Combining the cascading high tower triggers in 2008 is a bit complicated.  In d+Au there were 4 HT triggers with increasing thresholds, while in p+p there were 3.  The TCU deals with overlaps and prescales in a somewhat non-intuitive, and highly correlated way.  In every overlap region, it prescales at L0 by the minimum prescale, and then rescales (i.e. labeling the event as satisfying a trigger id) from this sample to create an unbiased distribution of the more strongly prescaled version.

For example, let's say we have HT4 prescaled at 1, HT2 prescaled at 2 and HT1 prescaled at 4.  If an event had a tower that satisfied HT4, the event would be kept and labeled with the HT4 trigger id.  Every 2nd event would also be labeled HT2, and every 4th event would also be labeled HT1.    Every other event that satisfies HT2 but not HT4 would be kept at L0, and FROM THIS POOL OF EVENTS every other event (4/2) would also be labeled HT1.   This is in contrast to the uncorrelated situation, in which the HT1 would be able to sample events that did not satisfy HT2 at L0.  This uncorrelated method is the way that the new TCU, hopefully in place for run 9, will work.

Note that this simple math can be invalidated by the existence of other triggers that can overlap with HT1 && (!HT2), but not HT2.

 So, in order to avoid double counting when combining triggers, the simplest thing to do is to look at what the event satisfied BEFORE prescales, i.e. at the last DSM.  Luckily, this information is available in the MuDst, in the quantity

 mu->event()->l0Trigger().dsmInput()

On a tower by tower basis, you can check with the StTriggerSimuMaker,

if (simuTrig->isTrigger(tidCheck)) {
        StTriggerSimuResult res = simuTrig->detailedResult(tidCheck);
        if (res.bemcDecision() == 1) {
        vector<short> towerIds = res.highTowerIds();

For d+Au 2008, the relevant bits are bht-bit0 == 7, bht-bit1 == 8, and bht4 == 9

For p+p 2008, the relevant bits are bht-bit0 == 6, bht-bit1 == 7

From Carl Gagliardi, the simple algorithm is:

HT4                                    Scale yield by 1/ps4 (almost always 1); correct for HT4  efficiency
HT2 && !(HT4)                   Scale yield by 1/ps2; correct forHT2 efficiency
HT1 && !(HT2 || HT4)                    Scale yield by 1/ps1; correct for HT1 efficiency
HT0 && !(HT1 || HT2 || HT4)             Scale yield by 1/ps0; correct for HT0 efficiency

where the first column is if the event satisfies the trigger id, and the second column is satisfying last DSM.

Unfortunately, in d+Au 2008 this does not work.  The problem is the Upsilon trigger, which runs off of HT2, which therefore is prescale 1 at L0.  This makes overlaps in events labeled as HT0 and HT1 not 100% correlated with events labeled as HT2; in principle the pendulum swings

the other way in this case, making the overlaps 100% uncorrelated, so the algorithm becomes: (again from Carl)

Assume HT0 with ps0, HT1 with ps1, and HT2 with ps2.  The assumption is that, thanks to the Upsilon trigger, these are all uncorrelated in the HT2 overlap region after we average over lots of runs that initialize the random select counters at various values.

Consider an event that passes the HT2 hardware threshold, but does not pass the HT4 hardware threshold.

We accept (1/ps2) of such events with HT2.

HT1 && !HT2 will accept (1/ps1) of the remaining events, for a total probability of
     [1 - (1/ps2)]*(1/ps1)

Thus, HT1 || HT2 accepts [(1/ps1)+(1/ps2)-(1/{ps1*ps2})] of the events.

In similar fashion, HT0 && !HT1 && !HT2 will accept (1/ps0) of the remaining events, for a total probability of:
    [1-(1/ps1)-(1/ps2)+(1/{ps1*ps2})]*(1/ps0)

If I've done the arithmetic correctly, that means HT0 || HT1 || HT2 will accept:
P_eff  =  (1/ps0) + (1/ps1) + (1/ps2)
              - (1/{ps0*ps1}) - (1/{ps0*ps2}) - (1/{ps1*ps2})
              + (1/{ps0*ps1*ps2})
of the events that are over the HT2 hardware threshold, but not over the HT4 threshold.  (Sanity check:  If one or more of ps0,ps1,ps2=1, then P_eff=1.  Good.)

1/P_eff is the effective prescale factor for this particular event class.

For pp 2008, there was no Upsilon, so the algorithm is simpler.

    my $bit0 = ($dsm & (1<<6))?1:0;
    my $bit1 = ($dsm & (1<<7))?1:0;
    $comb = $bit0 + 2*$bit1;
    my $tht2 = (($comb&3)==3) ? 1 : 0;
    my $tht1 = (($comb&2)==2) ? 1 : 0;
    my $tht0 = (($comb&1)==1 || ($comb&2)==2) ? 1 : 0;
  # Now start rejecting
    $keep = 0;
    if ($actids{220520}) {
      $keep = 4;
    }
    if ($actids{220510} &&
        !($tht2)) {
      $keep = 2;
    }
    if ($actids{220500} &&
        !($tht2) &&
        !($tht1)) {
      $keep = 1;
    }

Asking for keep>0 gets almost all of the data as taken; the rejected events are from overlaps from other triggers such as JP1, etc., which are rather rare.  I've managed to run through a small subset of the data, and get:

Total Events Rejected: 1871 out of 1714316:0.11%
220500
        1 1 0 0 644823 0 : 0.0 % Rejected
        2 1 1 0 77105 1718 : 2.2 % Rejected
        3 1 1 1 38643 17 : 0.0 % Rejected
         Rejected 1735 out of 760571: 0.23%
220510
        2 1 1 0 424746 0 : 0.0 % Rejected
        3 1 1 1 213781 136 : 0.1 % Rejected
         Rejected 136 out of 638527: 0.02%
220520
        3 1 1 1 642876 0 : 0.0 % Rejected
         Rejected 0 out of 642876: 0.00%
 

Note that there is a period of time where bht2, i.e. trigger id 220520, had a prescale !=1. 

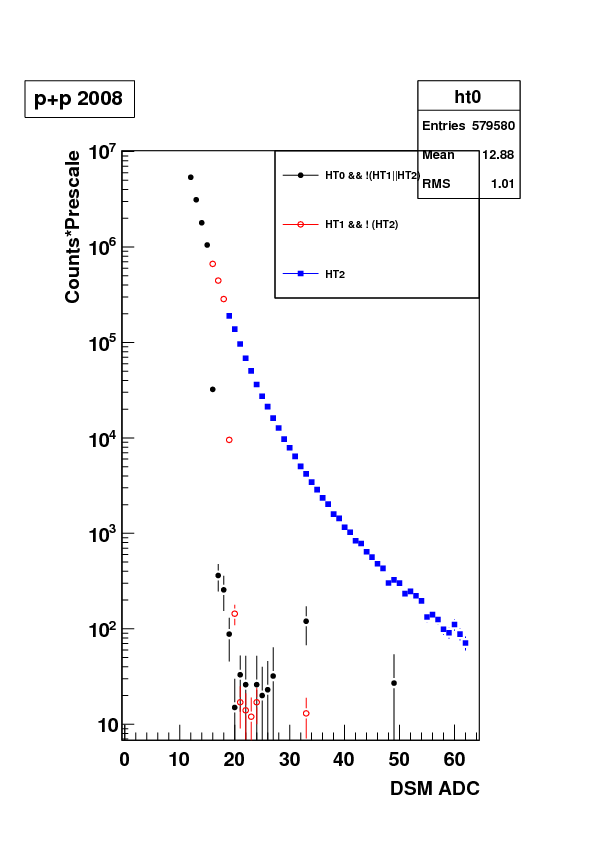
Taking the DSM ADC from the trigger simulator, you get the following for the algorithm. There appears to be some grass, e.g. towers that satisfy HT0 && !(HT1 || HT2) that have a DSM ADC > the HT1 threshold of 15, and the same for 18, but overall the distributions combine well. I have not gotten a chance to investigate the grass in detail; might be due to multiple towers satisfying in an event, or might be due to a slight mismatch between the trigger as actually run and the trigger simulator.

 In the d+Au, there are some issues in the HT2 overlaps, because of the Upsilon trigger at L2.  For example, in run 9023008, the prescale for the HT2 trigger was 2, but the Upsilon trigger was running at prescale 1.  This means that ~50% of the events that satisfy HT2, sampled by HT1 and HT0, were not labeled as HT2 (i.e. the uncorrelated case.)  Running the simple algorithm:

my $bit0 = ($dsm & (1<<7))?1:0;
    my $bit1 = ($dsm & (1<<8))?1:0;
    my $bit4 = ($dsm & (1<<9))?1:0;
    $comb = $bit0 + 2*$bit1 + 4*$bit4;
    my $tht4 = (($comb&4)==4) ? 1 : 0;
    my $tht2 = (($comb&3)==3) ? 1 : 0;
    my $tht1 = (($comb&2)==2) ? 1 : 0;
    my $tht0 = (($comb&1)==1 || ($comb&2)==2) ? 1 : 0;
 

my $keep = 0;
 if ($actids{210541}) {
   $keep = 8;
 }
 if ($actids{210521} &&
     !($tht4)) {
   $keep = 4;
 }
 if ($actids{210511} &&
     !($tht4) &&
     !($tht2)) {
   $keep = 2;
 }
 if ($actids{210501} &&
     !($tht4) &&
     !($tht2) &&
     !($tht1)) {
   $keep = 1;
 }
if ($keep == 0) reject

gives:

Total Events Rejected: 483 out of 8325:5.80%
210501
       1 1 0 0 0 2240 0 : 0.0 % Rejected
       2 1 1 0 0 274 0 : 0.0 % Rejected
       3 1 1 1 0 138 69 : 50.0 % Rejected
       7 1 1 1 1 3 0 : 0.0 % Rejected
       Rejected 69 out of 2655: 2.60%
210511
       2 1 1 0 0 1672 0 : 0.0 % Rejected
       3 1 1 1 0 837 422 : 50.4 % Rejected
       7 1 1 1 1 17 0 : 0.0 % Rejected
       Rejected 422 out of 2526: 16.71%
210521
       3 1 1 1 0 3774 0 : 0.0 % Rejected
       7 1 1 1 1 78 0 : 0.0 % Rejected
       Rejected 0 out of 3852: 0.00%
210541
       7 1 1 1 1 156 0 : 0.0 % Rejected
       Rejected 0 out of 156: 0.00%

This is an appreciable number of triggered events that could be recovered with the more complicated uncorrelated algorithm.  Need to check that this actually works over the full set of conditions.  There can be some odd effects from small prescales (i.e. 2 and 5 vs. 2 and 4), and randomization, but hopefully these wash out over the range of conditions taken.