Home » Blogs » jwebb's blog

EEmc Gammas via conversion method, improving hadronic veto

Updated on Thu, 2008-03-27 12:51. Originally created by jwebb on 2008-03-25 18:19.
 
Abstract:  Based on EEmc Gammas via conversion method, losses due to cuts we saw that the hadronic veto cut (sum of all postshower tiles w/ in R<0.3 is less than 0.2 MeV) reduces gamma yields by 50%, with events at higher pT suffering most.  Based on EEmc Gammas via conversion method, relaxing the hadronic veto cut, where we relaxed the hadronic veto, we saw odd behaviors in other variables which are suggestive of hadronic backgrounds.  In this study we examine using a ratio of postshower energy to candidate energy in place of the absolute cut.
 
Event sample:
 
1. Data from ppLong2
2. All fills after L2gamma EEmc elevated to physics
4. Select trigger ID 137641
 
Contents:
 

1.0 The Postshower Ratio Cut

 
The EEmc has 24 layers and a sampling fraction of about 5%.  Therefore the "fair share" energy deposited in each layer for any electromagnetic cascade would be about 1/500th of the energy of the particle (0.05 * 1/24 = 1/480).  So we try Log( 500 * Epost / Ecandidate) as a discrimination variable (the "discriminant").
 
To obtain a reasonably enriched gamma sample, we apply the following cuts:

1. Require candidate to be w/in the EEMC with pT > 5.0 GeV.

2. Isolation cut -- ET / ETR<0.3 > 0.9
3. Double charged particle veto -- require sum of all preshower-1 and preshower-2 tiles w/in R < 0.3 to be == 0
 

Figure 1.1 -- Ratio of energy deposited in postshower to energy of candidate plotted vs. candidate pT.  Data points show the mean of the distribution in each pT bin.
 

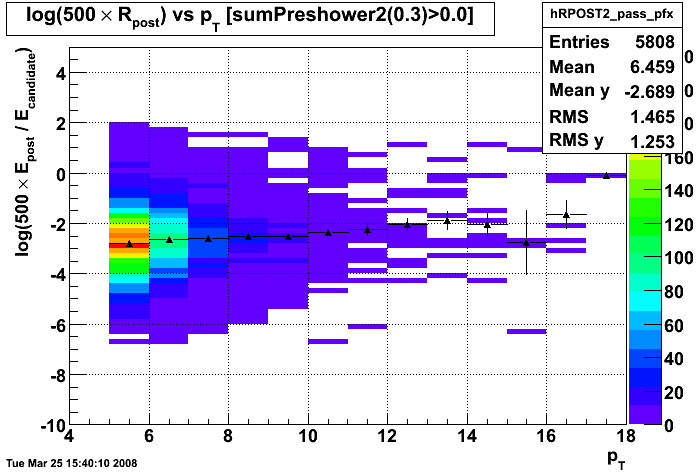
 Observations:
1. The mean of the discriminant increases slowly with pT.  This may indicate either (a) there is more background contamination at higher pT, or (b) the EM shower starts later and lasts longer at higher pT than at lower pT.
2. This discriminant may be better than an absolute cut on postshower energy.  The MC should be able to test this question.
 

Figure 1.2 -- Ratio of energy deposited in postshower to energy of candidate, evolution with cuts.  Isolation cut (red), preshower-1 cut (yellow), preshower-2 cut (green).

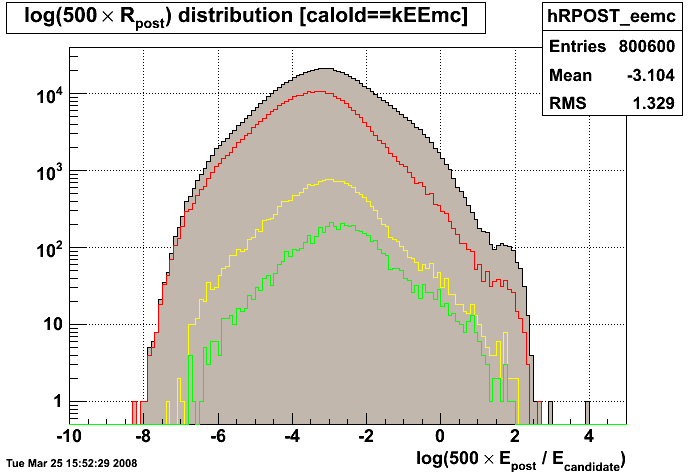
Observations:

1. There is a "bump" around 2 which is still present after both preshower cuts.
2. The slope seems to change around -1 or so.  At -1, this is like saying that the postshower detector sees 10% of it's "fair share" energy of a single photon.
3. Values >= 0 on this plot should probably be treated as background -- EM showers should be reasonably well contained at this point.

 

A better discriminant could involve the SMD energy instead of the tower energy.  Specifically, the backgrounds which I am concerned about at present tend to have small energy deposits in the SMD relative to the tower energy.  They tend to be rejected reasonably well by applying the absolute veto on the postshower detector.  So perhaps a ratio of postshower to SMD energy would single out these events better. 

 

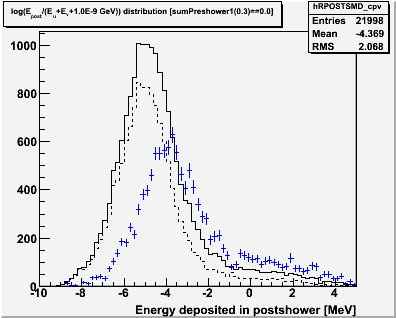
2.0 The Postshower-SMD Ratio Cut

 

Form a discriminant combining both postshower response and SMD response. 

D = Log( Epost / ( Eu+Ev+1.0E-9 GeV) )

Events with large postshower energy relative to the SMD should show up at larger values of the discriminant.  The value of 1.0E-9 GeV added to the denominator is there so that zero SMD energy is handled gracefully (i.e. it get cut, likely showing up in the overflow bin of the histogram).

Figure 2.1 -- Postshower-to-SMD energy ratio.

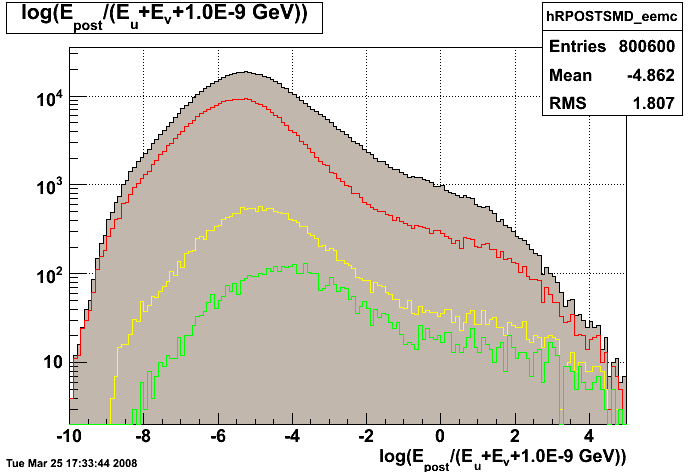
Observations:
1. There is a clear change in behavior of this discriminant at ~ -1.0.
2. It may be possible to estimate the contribution of this background by fitting this distribution to the sum of two gaussians.

 

3.0 Conversion Method w/ Post-SMD Ratio Cut

 
Below we show the evolution of shower-shape distributions as cuts are applied.  The order of the cuts, and the color coding, are --
 
Cuts:
1. BLACK:     Require candidate to be w/in the EEMC with pT > 5.0 GeV.
2. BLUE:        Isolation cut -- ET / ETR<0.3 > 0.9
3. RED:          Hadron cut -- Log( Epost/(Eu+Ev+1.0E-9 GeV) ) < -1.0
4. YELLOW:  Charged particle veto (CPV) -- sum of all preshower-1 tiles w/in R < 0.3 of gamma candidate == 0.
5. GREEN:     Analyzing cut -- sum of all preshower-2 tiles w/in R < 0.3 of gamma candidate > 0
 

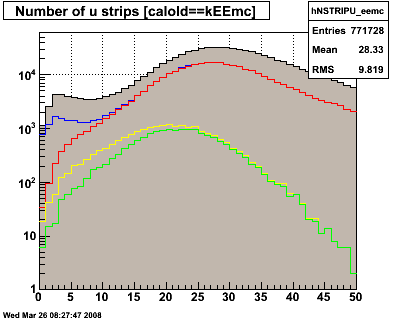
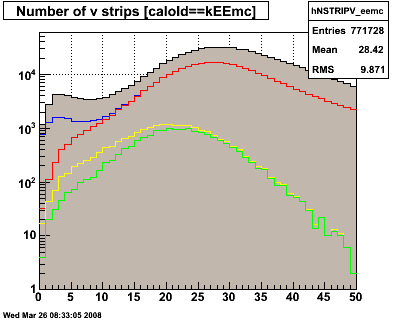
Figure 3.1 -- N smd strips above 3 sigma + ped.  U plane (left), V plane (right).
 
Observations:
1. The new postshower/smd cut is, for many events, no more restrictive than the isolation cut.  eg nu > 10 || nv > 10. 
2. It significantly reduces (but does not eliminate) the event class we are worried about -- events which deposit energy in only a few strips of the SMD.
 

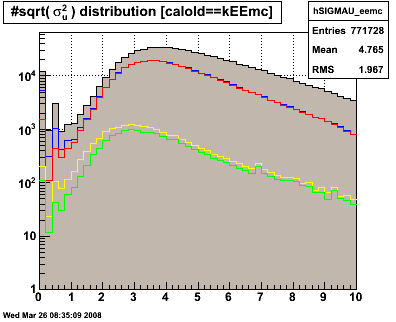
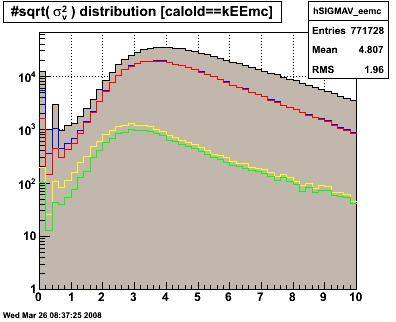
Figure 3.2 -- SMD widths.  Uplane (left), Vplane (right).
 
 
Observations:
1.  The problematic events at low widths are reduced, but not eliminated.
 

Figure 3.3 -- Ratio of SMD to candidate energy.  Uplane (left), Vplane (right).
 

Observations:

1. The improvement here is more difficult to see... but the events which show up with no energy in the SMD relative to the gamma candidate are significantly supressed.  Although once again, they are not eliminated entirely.

 

4.0 Fit to the Post-SMD ratio distribution

Figure 4.1 -- Fit the postshower-SMD ratio distribution to the sum of two gaussians to estimate the fraction of events which may be due to hadronic showers.  (Note: the hadron fraction is calculated over the range [10,-1), not [10,1) as the figure suggests.)

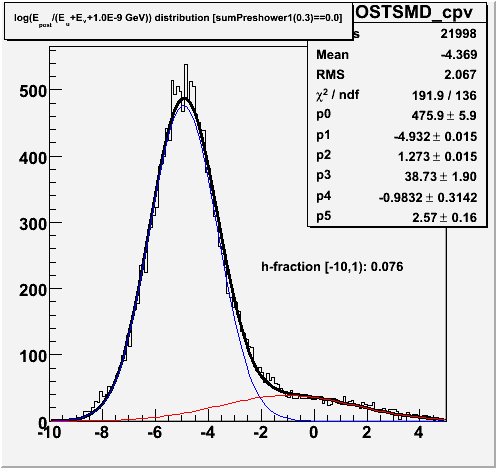
Observations / Thoughts:
1. 7.6% of the events which pass the charged-particle veto and my first try at cutting on this variable look like they are charged or neutral hadrons which shower in the endcap.
2. How much would this effect the gamma extraction?  That requires some assumptions.
 
    a. If we assume that 1/2 of the events with R<-1.0 are photons, then the remainer are background.  7.6% of the total is this neutral-or-charged hadron background.  So about 42.4%
        will be pi0, eta and other electromagnetic backgrounds.
    b. Then the background is ~85% photonic, and 15% hadroinc (i.e. particles which interact hadronically in the calorimeter).
  
    How does this alter our efficiencies for backgrounds to pass the analyzing cut on the 2nd preshower detector?
 
   + εphotonic = 92.5% as originally estimated
   + εhadronic = 50.0%, which I "read off" from figure 2.1
   + Therefore our actual background efficiency is εb = 0.85 * εphotonic + 0.15 * εhadronic = 78.7%
 
    We know from EEmc Gammas via conversion method, chi2 comparison that a 5% systematic uncertainty in the background efficiency corresponds to a ~30% systematic uncertainty in the yields.  The
    systematic uncertainty given by this background source is about 15% in terms of the detection efficiency, which translates into a 100% systematic uncertainty in the yield.
    This is a problem.  To illustrate, here is the photon-extraction plotted vs. this post-smd ratio:
 
Figure 4.1 -- Gamma extraction vs. post-smd ratio.  It illustrates that the extraction method fails in the presence of a significant hadronic background.
 
 Observations
1. It illustrates that the extraction method fails in the presence of a significant hadronic background.
 
Also, note that it will be important to measure backgrounds inline with the data rather than trust pythia/geant simulations.  See this thread on high-pT.
 
 

5.0 Conclusions, questions

1. The Postshower-to-SMD energy cut should be a reasonable method for discriminating against hadronic showers.
2. Assuming  that the EM & hadronic showers can be each be reasonably described by a gaussian, then a reasonable cut should be able to achieve a reasonable purity for photons.
3. The conversion method fails on this class of "hadronic shower-like" events.  It fails because we get the background efficiency wrong.
4. Questions about the background which need to be answered:
     (1) what type of particles?  (2) how likely do they satisfy the analyzing cut? (3) how does the composition (and therefore efficiency for detecting) the background change with 
     various discrimination variables (e.g. chi^2, SMD residuals, etc...).
5. Can I come up with a "better" discriminant?  Some things to look at:
     (1) Number of postshower tiles > threshold (2) ...

 

 

 

»