2006 EEMC Neutral Pions: New Trees with Fill TPC Runs
It was decided in the ANL-VU meeting that we would proceed toward a preliminary result utilizing the most recent trees and the new TPC run list. Here, I present the status of the transverse asymmetries having integrated these new runs using the newest trees.
Figure 1
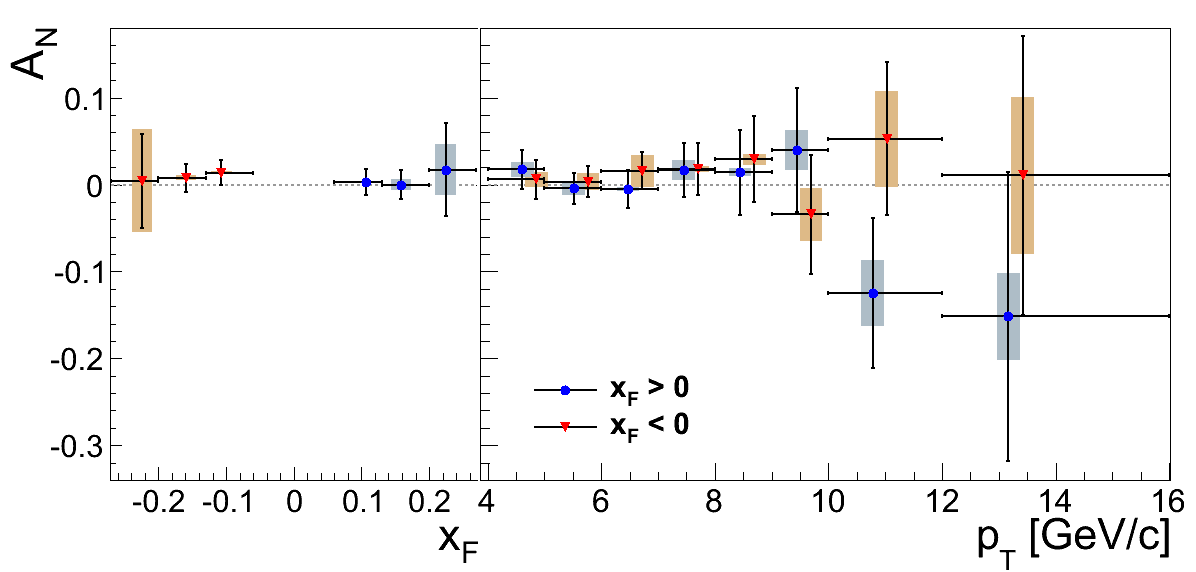
The asymmetries still measure zero. Perhaps, the additional statistics are smoothing out some of the fluctuation in pT.
Figure 2
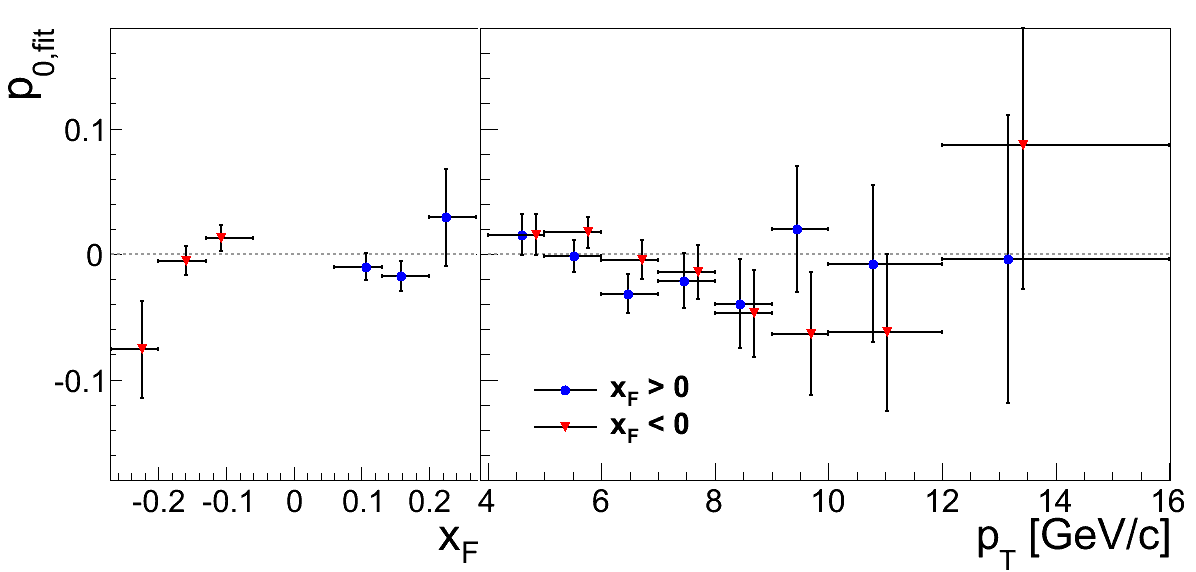
Table 1
| pT Blue | pT Yellow | xF Blue | xF Yellow | |
|---|---|---|---|---|
| χ2/ν | 6.01006/7 | 8.21802/7 | 1.38496/2 | 5.59658/2 |
| p0 | -0.00907574±0.00758638 | 0.0022855±0.00745623 | -0.0117242±0.00767894 | 0.00158432±0.0075207 |
Here, I have fit the p0 distributions with a constant. The offsets for the blue beam xF and pT fits are 1.53σ and 1.2σ from zero, respectively. The χ2 for the yellow beam xF fit is 1.87σ from expectation.
Figure 3
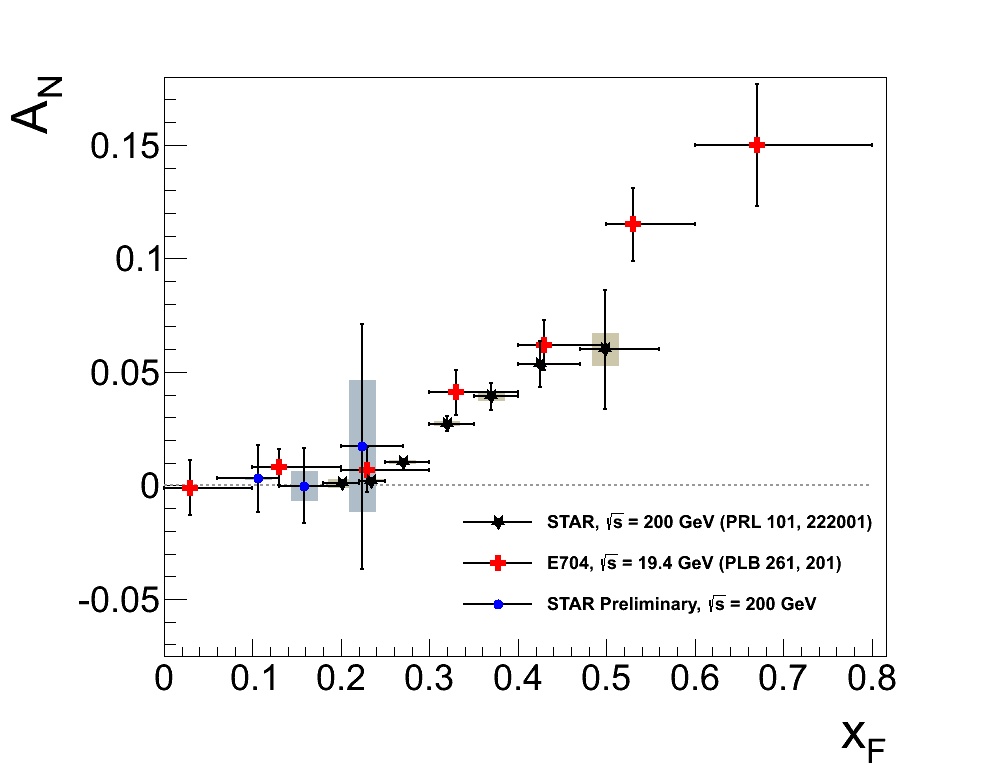
Figure 3 shows our data compared with previous publications, namely STAR FPD data and E704 data. PHENIX has preliminary results for neutral-energy clusters at forward pseudorapidity which pick up at xF = 0.25. To be clear, our results are not yet "STAR Preliminary." The data have been so labeled solely for clarity.
Table 2: xF > 0
| AN | δAN Stat | δAN Total Syst | δAN B.g. Asym Syst | δAN Mass Window Syst | |
|---|---|---|---|---|---|
| xF Bin 1 | 0.0031 | 0.0147 | 0.0008 | 0.0008 | 0.0001 |
| xF Bin 2 | -0.0001 | 0.0164 | 0.0067 | 0.0013 | 0.0065 |
| xF Bin 3 | 0.0172 | 0.0538 | 0.0290 | 0.0036 | 0.0288 |
| pT Bin 2 | 0.0173 | 0.0230 | 0.0092 | 0.0000 | 0.0092 |
| pT Bin 3 | -0.0044 | 0.0179 | 0.0082 | 0.0008 | 0.0081 |
| pT Bin 4 | -0.0050 | 0.0219 | 0.0021 | 0.0015 | 0.0015 |
| pT Bin 5 | 0.0170 | 0.0309 | 0.0114 | 0.0020 | 0.0113 |
| pT Bin 6 | 0.0139 | 0.0489 | 0.0047 | 0.0026 | 0.0039 |
| pT Bin 7 | 0.0395 | 0.0712 | 0.0233 | 0.0028 | 0.0231 |
| pT Bin 8 | -0.1247 | 0.0865 | 0.0381 | 0.0026 | 0.0380 |
| pT Bin 9 | -0.1516 | 0.1664 | 0.0501 | 0.0031 | 0.0500 |
Again, the systematic uncertainties include adjusting the background asymmetry and mass window. The statistical uncertainties include uncertainties from the fit parameters, previously included in both statistical and systematic uncertainties. In one bin, the background asymmetry systematic leads, while the mass window leads nine other bins. In one bin the systematic uncertainty is evenly split. In all eleven bins, the statistical uncertainties are larger than the systematic uncertainties.
Table 3: xF < 0
| AN | δAN Stat | δAN Total Syst | δAN B.g. Asym Syst | δAN Mass Window Syst | |
|---|---|---|---|---|---|
| xF Bin 1 | 0.0135 | 0.0144 | 0.0018 | 0.0016 | 0.0007 |
| xF Bin 2 | 0.0078 | 0.0160 | 0.0030 | 0.0026 | 0.0014 |
| xF Bin 3 | 0.0044 | 0.0541 | 0.0591 | 0.0073 | 0.0586 |
| pT Bin 2 | 0.0061 | 0.0227 | 0.0084 | 0.0001 | 0.0084 |
| pT Bin 3 | 0.0033 | 0.0176 | 0.0099 | 0.0016 | 0.0098 |
| pT Bin 4 | 0.0158 | 0.0215 | 0.0182 | 0.0029 | 0.0179 |
| pT Bin 5 | 0.0176 | 0.0299 | 0.0037 | 0.0037 | 0.0003 |
| pT Bin 6 | 0.0291 | 0.0495 | 0.0062 | 0.0057 | 0.0022 |
| pT Bin 7 | -0.0345 | 0.0685 | 0.0310 | 0.0047 | 0.0306 |
| pT Bin 8 | 0.0526 | 0.0881 | 0.0552 | 0.0072 | 0.0547 |
| pT Bin 9 | 0.0106 | 0.1608 | 0.0906 | 0.0061 | 0.0904 |
For one bin of xF < 0, the systematic uncertainty is larger than the statistical uncertainty. Likely, we can better constrain this uncertainty by examining multiple mass windows and calculating a sort of standard deviation. This will be left for the final results. In four bins, the background asymmetry leads, while for the other seven, the mass window leads.
Figure 4
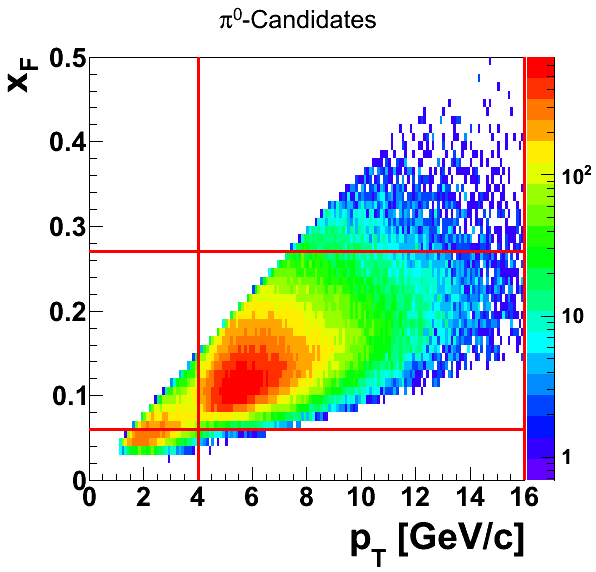
In Fig. 4 I show the kinematic scatter plot for the pion candidates. The cut ranges are shown in red.
Run List
7097009 7097010 7097014 7097017 7097018 7097019 7097020 7097021 7097024 7097025 7097026 7097027 7097032 7097093 7097094 7097095 7097096 7097097 7097099 7097102 7097103 7097104 7097105 7098001 7098002 7098004 7098006 7098007 7098008 7098014 7098015 7098018 7098024 7098025 7098027 7098028 7098029 7098031 7098032 7098033 7098034 7098036 7098038 7098039 7098040 7098041 7098053 7098055 7098061 7098062 7098064 7098065 7098066 7098067 7098072 7098073 7098074 7098075 7098079 7098080 7098081 7098082 7098083 7099003 7099006 7099014 7099015 7099016 7099021 7099022 7099024 7099025 7099026 7099027 7099030 7099031 7099033 7099034 7099035 7099047 7100014 7100015 7100016 7100028 7100029 7100031 7100052 7100055 7100058 7100062 7100064 7100067 7100068 7100070 7100071 7100072 7100075 7100076 7100077 7100078 7101013 7101015 7101019 7101023 7101025 7101039 7101041 7101042 7101046 7101050 7101052 7101054 7101075 7101078 7101082 7101085 7101086 7103006 7103007 7103008 7103013 7103014 7103016 7103017 7103018 7103024 7103026 7103027 7103030 7103040 7103072 7103073 7103075 7103077 7103078 7103080 7103081 7103082 7103086 7103087 7103088 7103089 7103090 7103093 7103095 7103096 7103099 7104014 7104016 7115011 7115024 7115085 7115086 7115087 7115088 7115089 7115095 7115097 7115099 7115101 7115103 7115106 7115111 7115113 7115114 7115115 7115116 7115117 7115121 7115122 7115124 7115125 7115126 7115130 7115131 7115134 7115137 7116044 7116050 7116052 7116057 7116059 7117002 7117008 7117009 7117010 7117011 7117015 7117016 7117017 7117027 7117050 7117056 7117057 7117058 7117060 7117063 7117064 7117067 7117068 7117069 7117071 7118002 7118003 7118004 7118008 7118009 7118010 7118014 7118016 7118017 7118024 7118026 7118032 7118033 7118035 7118038 7118039 7118041 7118042 7118044 7118045 7118048 7118049 7118050 7118051 7118053 7118073 7118075 7118077 7118083 7118084 7118085 7118087 7118088 7118092 7119001 7119002 7119003 7119004 7119019 7119020 7119021 7119022 7119028 7119032 7119065 7119068 7119069 7119079 7119080 7119082 7119084 7119085 7119088 7119090 7119091 7120023 7120045 7120046 7120047 7120049 7120053 7120082 7120085 7120088 7120089 7120091 7120092 7120093 7120100 7120101 7120112 7120113 7120116 7120117 7120121 7120128 7120129 7120131 7120132 7120133 7121001 7121007 7121012 7121013 7121015 7121016 7121020 7121021 7121024 7121038 7121041 7121043 7121118 7121119 7121120 7121122 7122002 7122003 7122004 7122035 7122037 7122043 7122044 7122045 7122046 7122047 7122048 7122049 7122053 7122054 7122056 7122057 7122058 7122069 7122070 7123014 7123015 7123019 7123020 7123022 7123024 7123025 7123027 7123028 7123030 7123031 7123032 7124009 7124016 7124018 7124021 7124024 7124026 7124029 7124031 7124034 7124063 7125005 7125013 7125014 7125015 7125016 7125017 7125018 7125021 7125022 7125023 7125028 7125044 7125052 7125053 7125055 7125056 7125057 7125058 7125059 7125061 7125066 7125067 7125069 7125070 7126008 7126009 7126010 7126011 7126012 7126016 7126019 7126022 7126023 7126025 7126036 7126037 7126056 7126057 7126058 7126059 7126062 7126063 7126064 7126065 7127001 7127005 7127006 7127007 7127009 7127010 7127011 7127033 7127037 7127038 7127039 7127041 7127042 7127045 7127046 7127049 7127050 7127067 7127069 7127072 7127073 7127075 7127076 7127077 7127080 7127087 7127090 7127092 7127096 7128001 7128002 7128005 7128006 7128007 7128008 7128009 7128013 7128023 7128024 7128025 7128028 7128032 7128045 7128046 7128048 7128050 7128051 7128057 7128059 7128061 7128063 7129001 7129002 7129003 7129009 7129018 7129020 7129021 7129023 7129027 7129031 7129032 7129035 7129036 7129041
- drach09's blog
- Login or register to post comments