- drach09's home page
- Posts
- 2022
- 2020
- June (1)
- 2019
- 2018
- 2017
- 2016
- 2015
- 2014
- December (13)
- November (2)
- October (5)
- September (2)
- August (8)
- July (9)
- June (7)
- May (5)
- April (4)
- March (4)
- February (1)
- January (2)
- 2013
- December (2)
- November (8)
- October (5)
- September (12)
- August (5)
- July (2)
- June (3)
- May (4)
- April (8)
- March (10)
- February (9)
- January (11)
- 2012
- 2011
- October (1)
- My blog
- Post new blog entry
- All blogs
Run-11 Transverse Jets: Revisiting Trigger Bias (part II)
Another check for trigger bias is to use simulation. With the small sample of embedding for 2011 it is probably not possible to extract meaningful bias information in great detail. However, it is perhaps possible to lean some broad limits as well as provide another sanity check for data-driven methods. For this study, I follow the procedure Kevin followed for the 2012 preliminary analysis. In the embedding, I match detector jets to particle jets and parton jets. I then match the parton jet to lines 7 or 8 of the PYTHIA record (all associations using the minimum η-φ distance and requring it to be less than 0.5). These are sorted into quark, anti-quark, and gluon jets. The same is done for my high-statistics PYTHIA sample, now, matching particle jets to parton jets and lines 7 or 8. The embedding cuts on pT and physics η are retained for the PYTHIA study, but all other cuts are released. I look at the break-down of the fractions of quark, anti-quark, and gluon jets for biased and unbiased samples and also the ratio of the biased and unbiased fractions. In the end, I average the ratios across the range of the "low," "mid," and "high" pT bins.
Figure 1: VPDMB
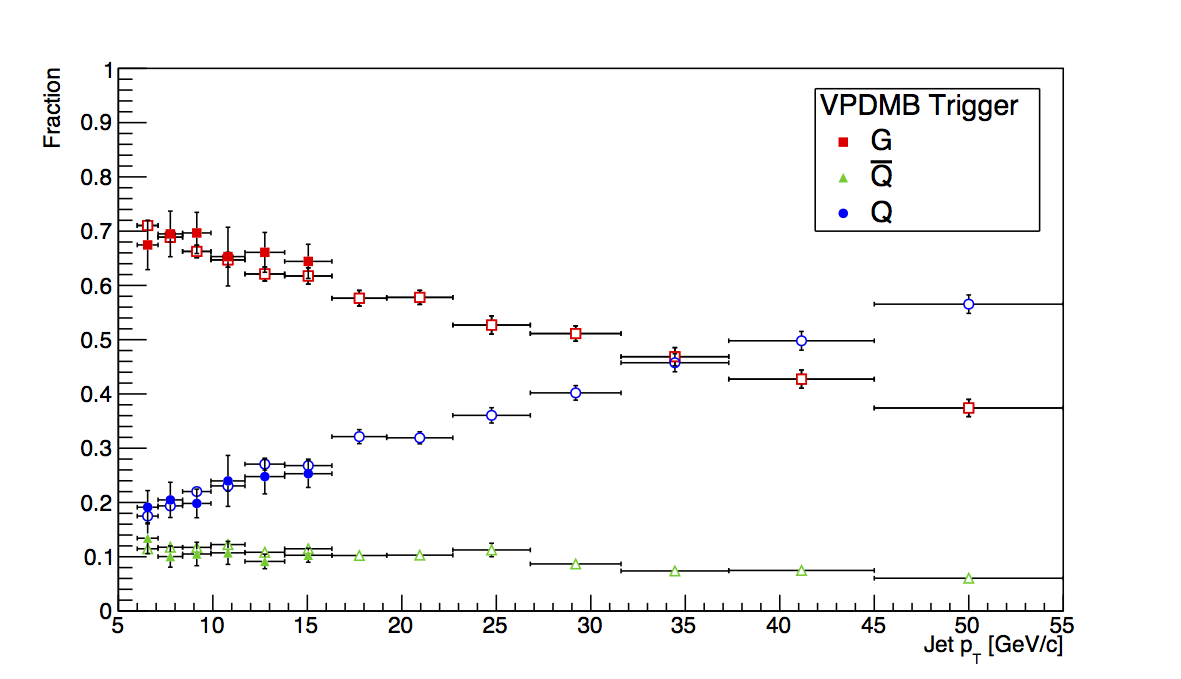
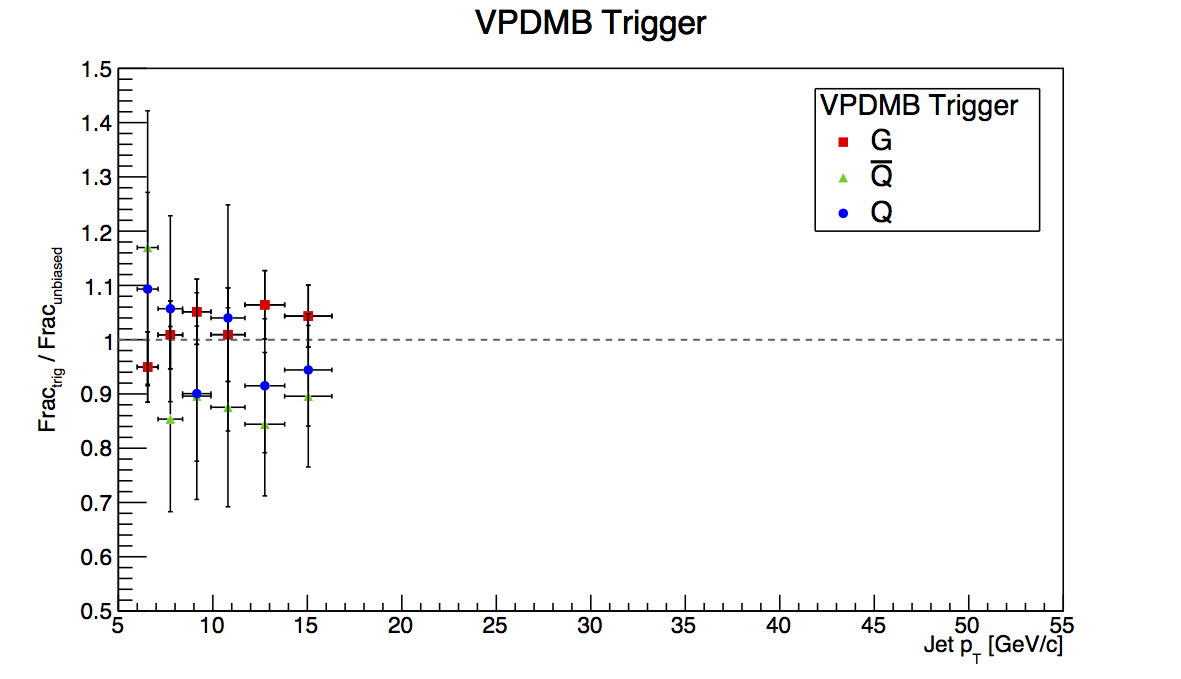
Figure 1 shows the plots for VPDMB. There is no trigger simulator for the min-bias condition, thus, one expects very similar behavior between VPDMB embedding and pure PYTHIA. Indeed, that is observed and seems to be a first-order sanity check for the method.
Figure 2: JP0
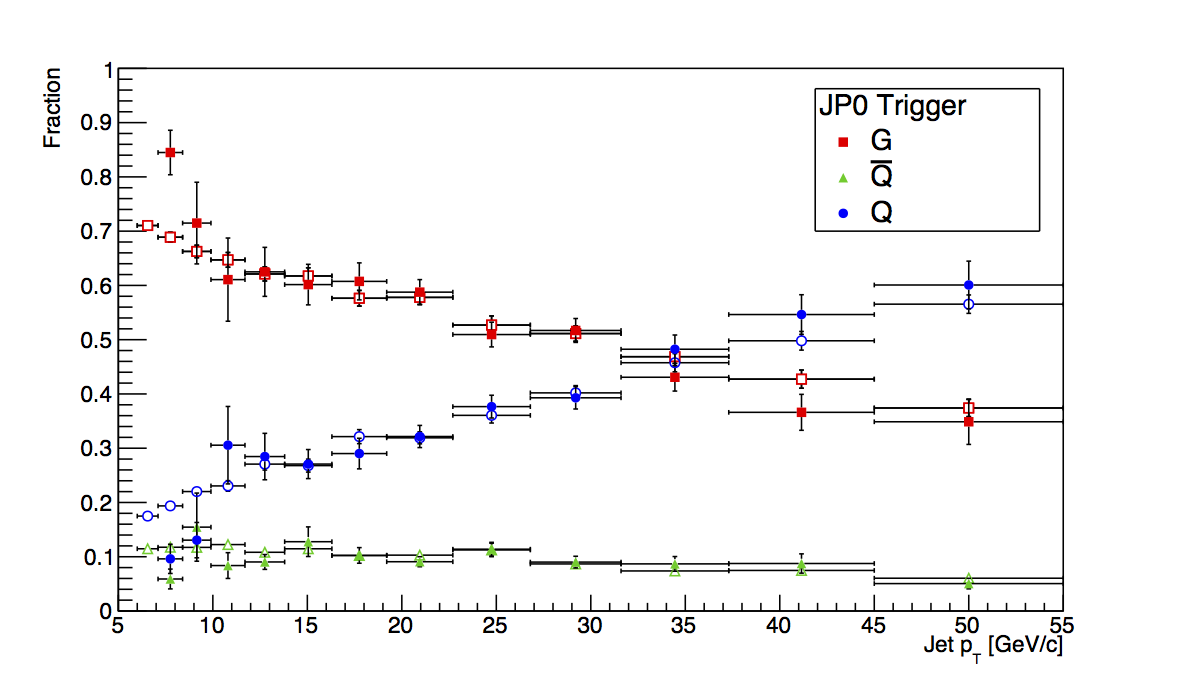
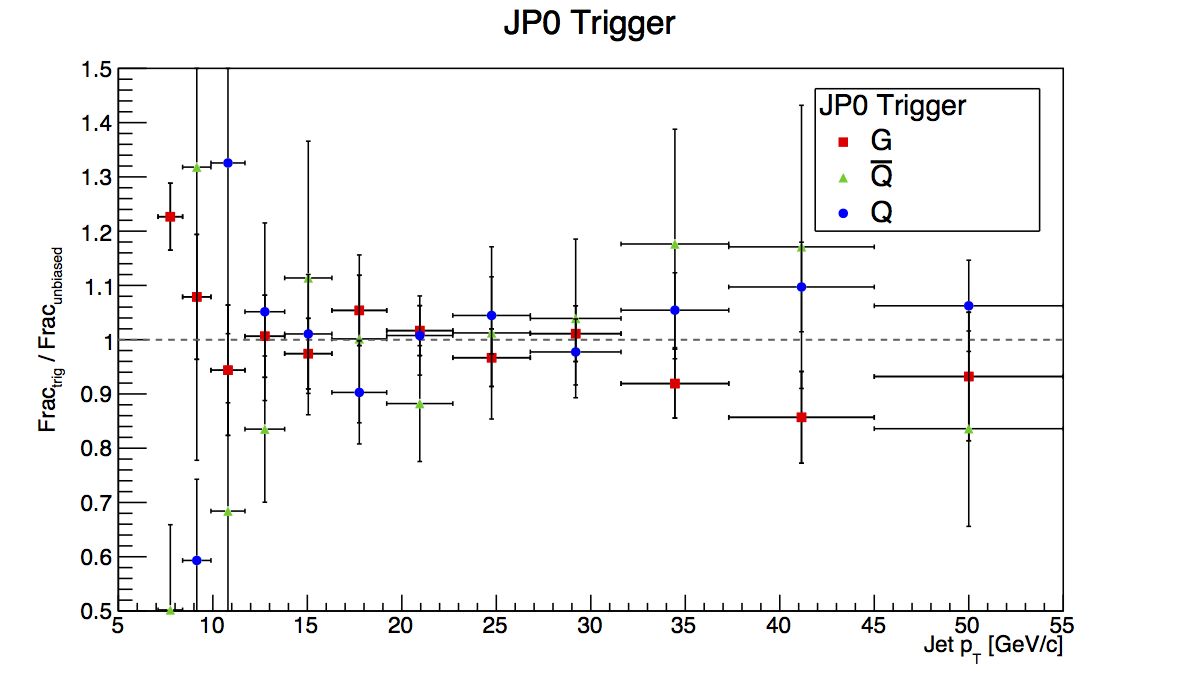
Figure 2 shows the plots for JP0. The first bin shows a rather large deviation between embedding and PYTHIA, however, it is certainly in the wrong direction for the known trigger bias. My two thoughts for this are either this is just an unlucky fluctuation due to finite statistics or it is a sign of more trigger emulator funny-business. Either way, it makes it difficult to trust this for a trigger-bias study when we know this is not the bias the trigger should introduce.
Figure 3: JP1
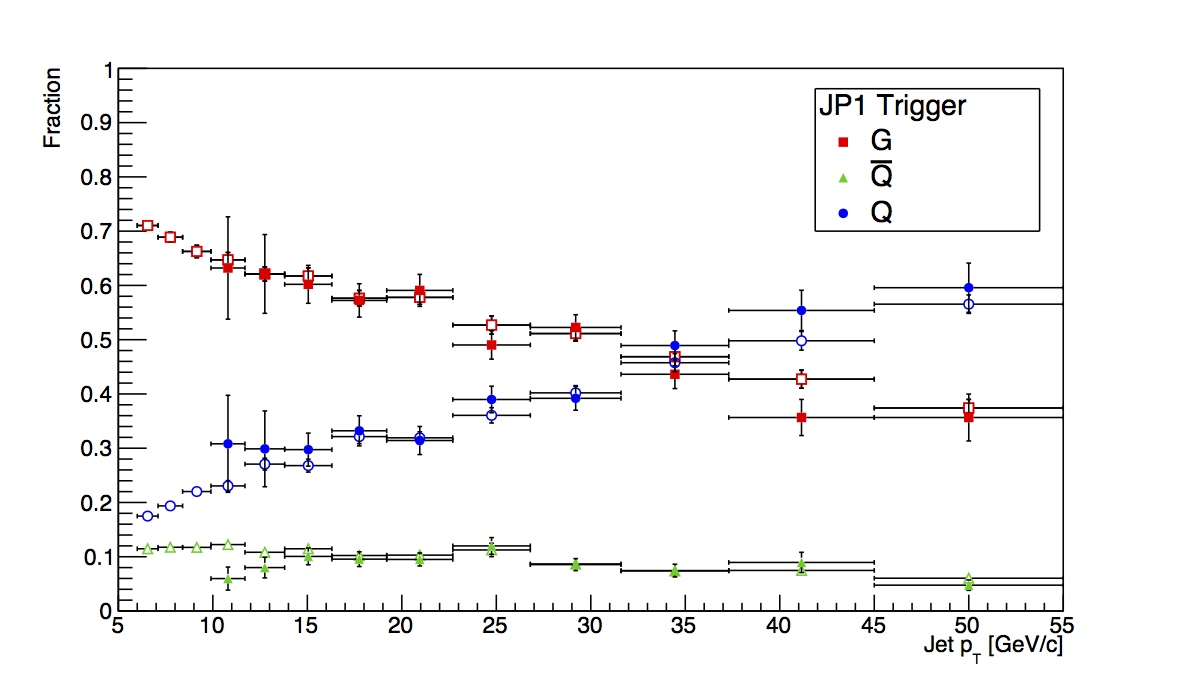
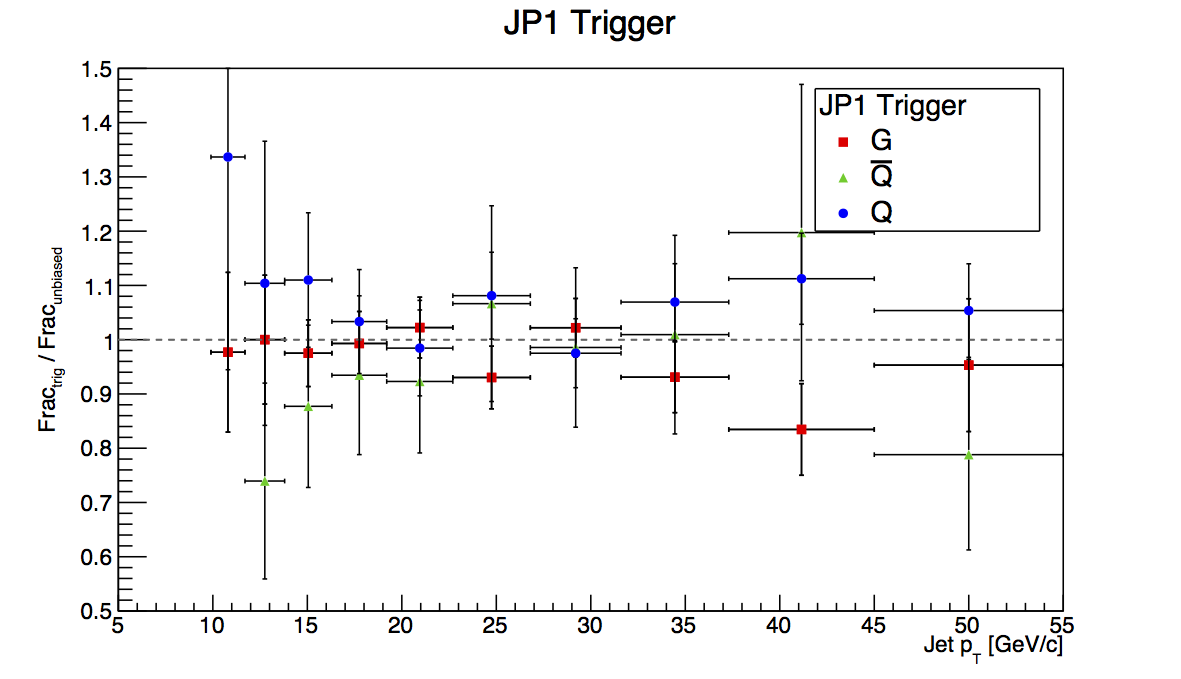
Figure 3 shows the plots for JP1, and the situation is more sensible than for JP0. Statistics are still limited at the trigger turn-on, but the flucutations are easier to swallow. Also, they tend to go more in the direction one might expect. Unfortunately, there are not nearly enough statistics, here, to place meaningful detailed limits on trigger bias.
Figure 4: JP2
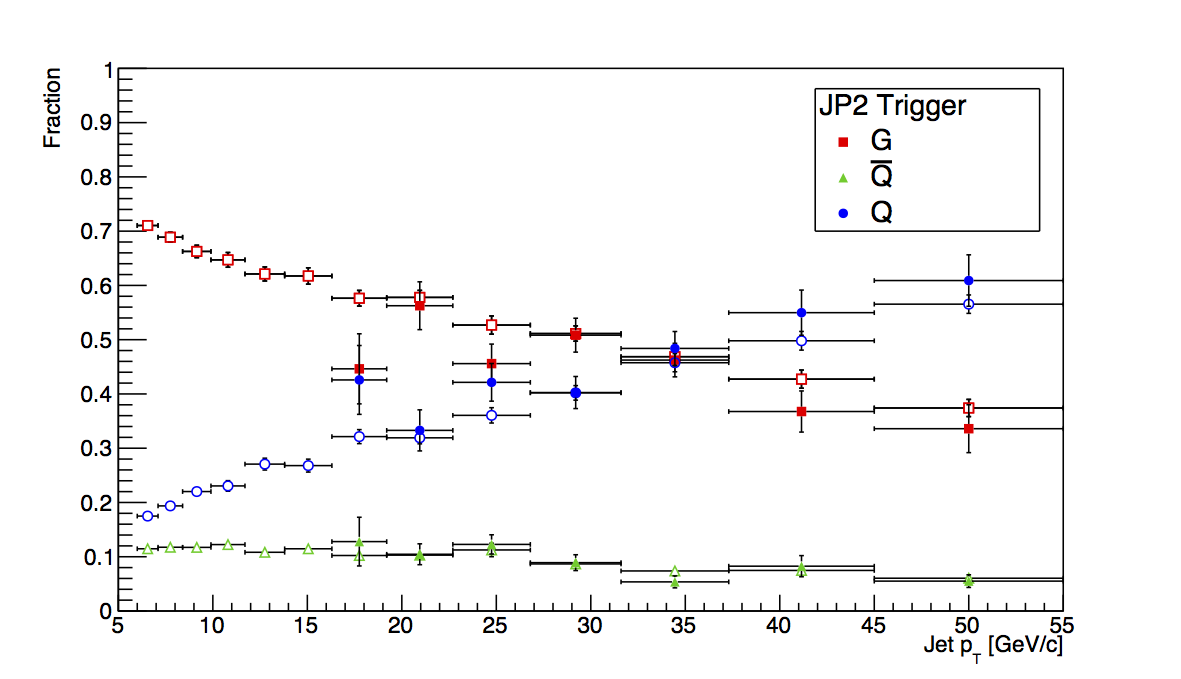
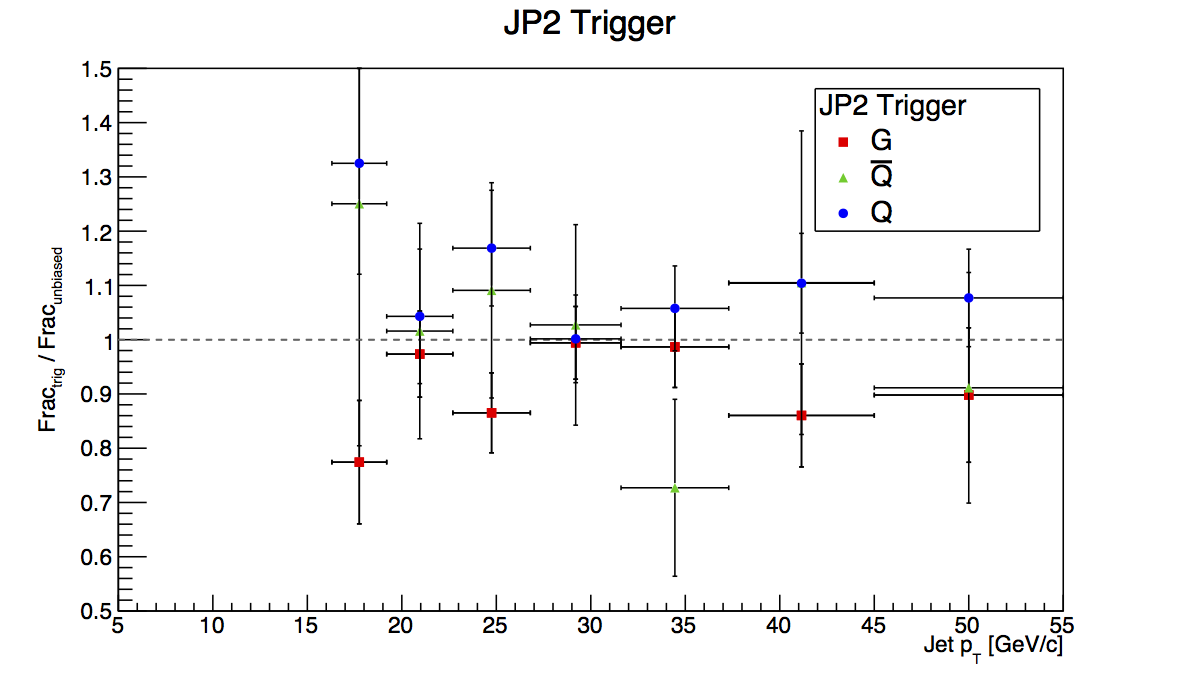
Figure 4 shows the plots for JP2. Again, it is difficult to put detailed limits on the bias with the given statistics.
Figure 5: Fitted Results
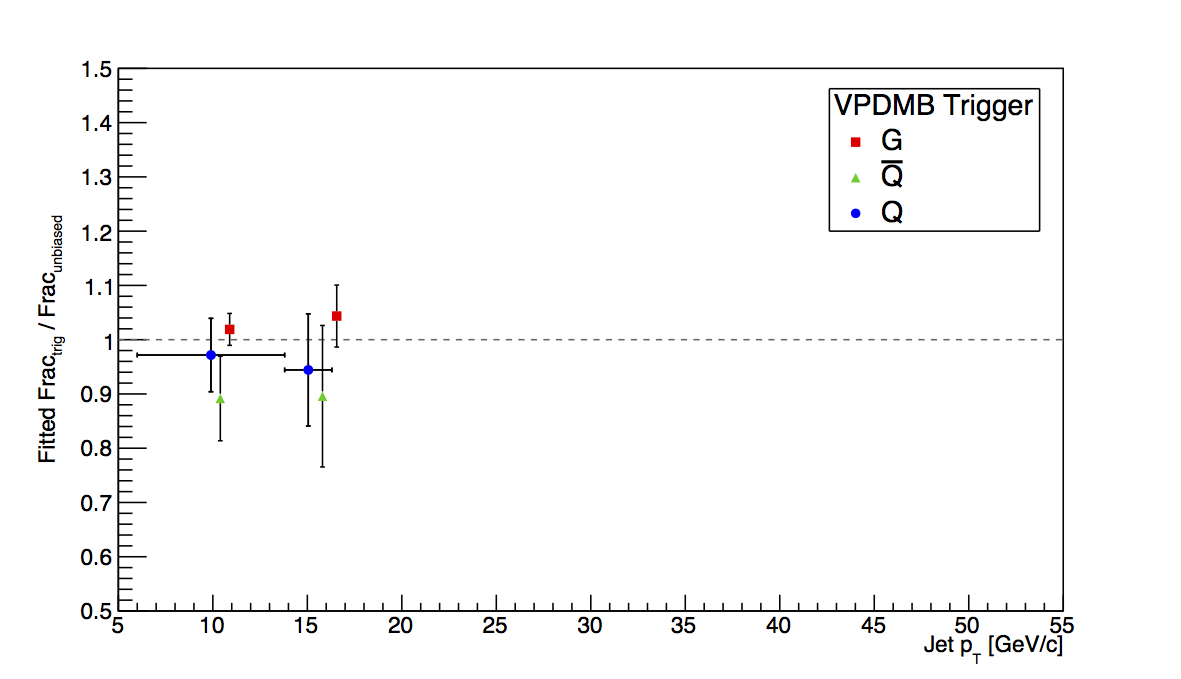
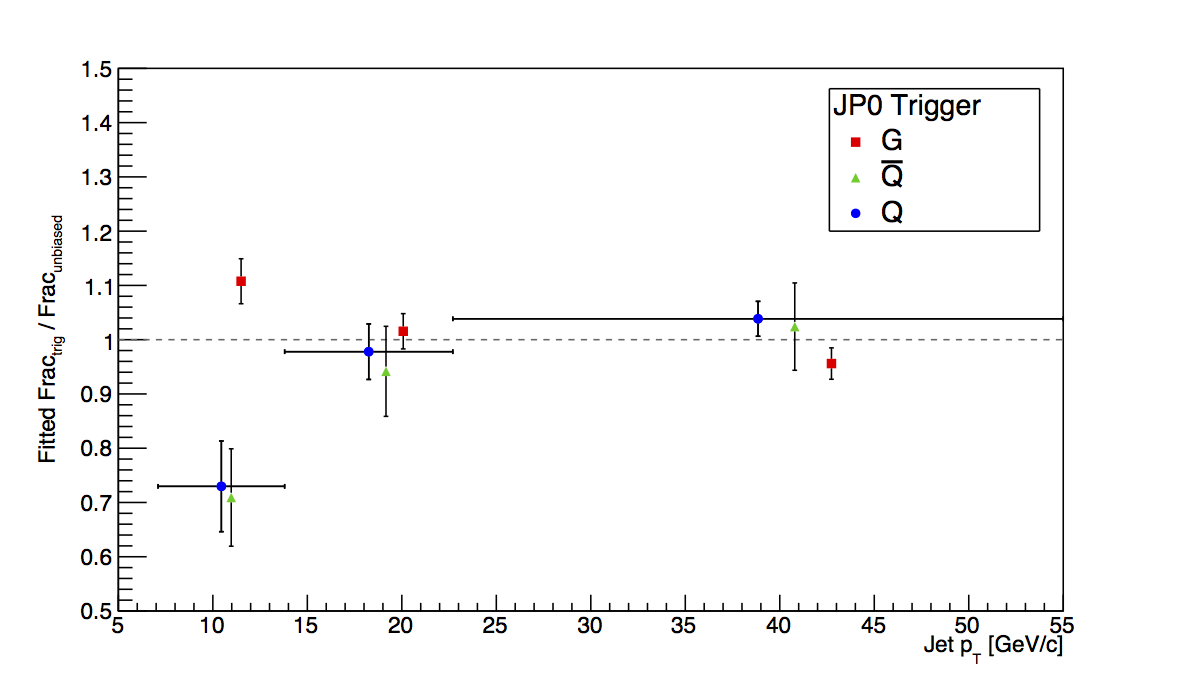
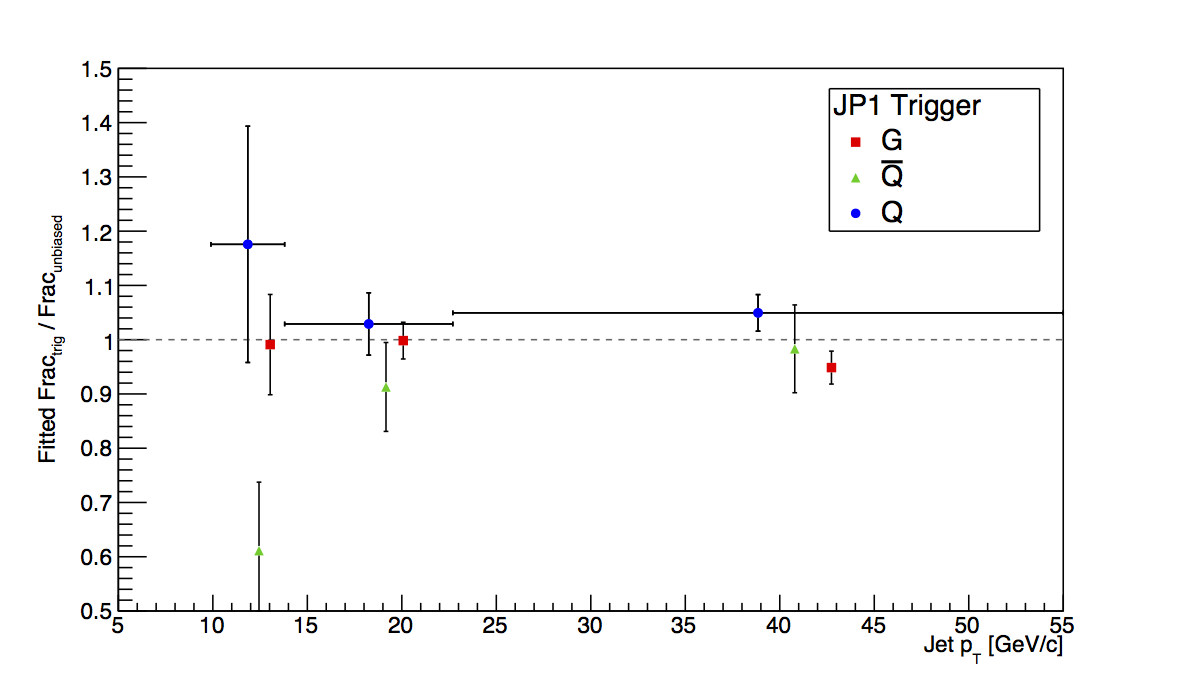
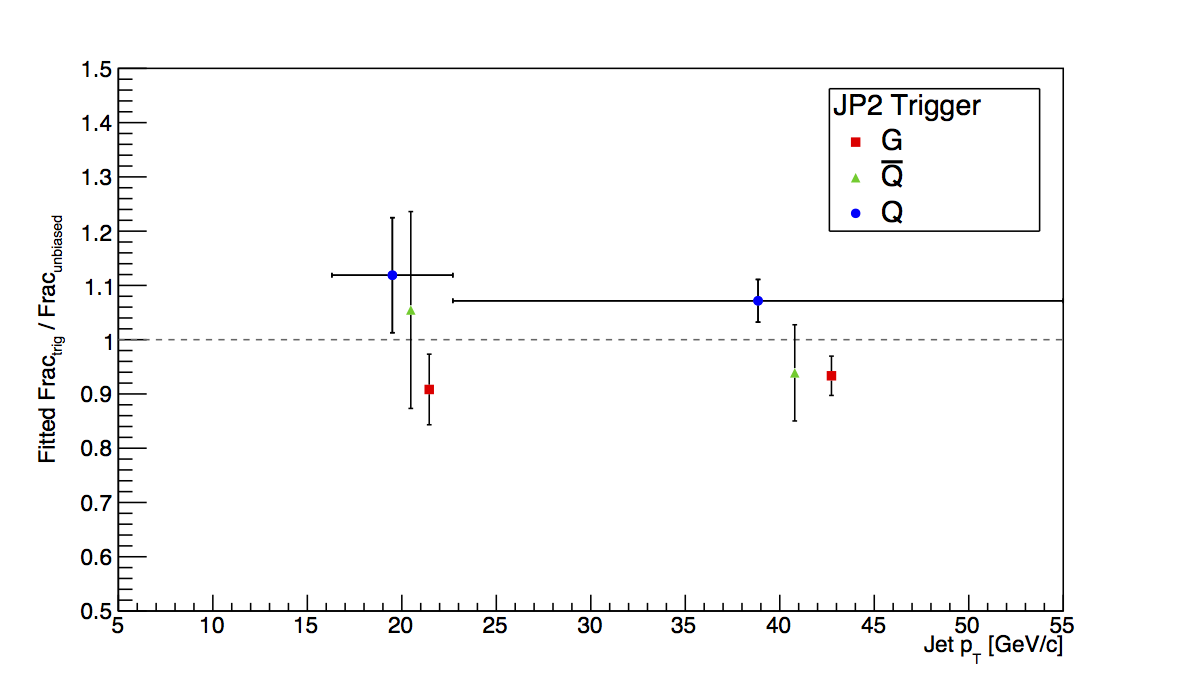
Figure 5 shows the result of fitting the ratio of the biased to unbiased fractions over the "low," "mid," and "high" pT bins. Fitting seems to give a bit better chance to quantify the low-pT bias.
Table 1: Fitted Gluon-jet Ratios
| Trigger | Low pT | Mid pT | High pT |
| JP0 | 1.108±0.041 | 1.016±0.032 | 0.956±0.029 |
| JP1 | 0.991±0.092 | 0.998±0.034 | 0.949±0.030 |
| JP2 | N/A | 0.908±0.065 | 0.933±0.036 |
It seems that perhaps one could take the least constrained triggers for the upper-limits on trigger bias for the broad pT ranges. Again, I don't trust the JP0 estimate, and might prefer to look at the data for that trigger. On the other hand, JP1 does contribute a large amount to low pT and the 9% uncertainty might be in the right ballpark, at the end of the day. For mid-pT, JP2 should exhibit the most bias. I could envision taking the deviation and uncertainty in quadrature as an upper limit, i.e. [(1-0.908)2 + 0.0652]1/2 = 0.11. For high-pT, the upper limits appear to be, again, from JP2. Following the mid-pT strategy, I would cite 0.076. However, I believe this number to be too large based upon Kevin's and Pibero's studies with better embedding statistics at 200 GeV. I believe that limit has to be closer to 2-5%.
Conclusions
- It is clearly difficult to quantify the low-pT trigger bias with the existing embedding sample. Some limits may be possible integrating over wide kinematic ranges. Otherwise, data-driven methods, as done for the preliminary result, are probably our best bet.
- There certainly seems to be something funny going on in JP0.
- I am struck by the fact that even as high as 25 GeV/c, gluons contribute over half the jet yield. Thus, even at low-pT, where the efficiency is lower for gluons than for quarks, there simply are not many quarks available. Throw on top of this the fact that we observe no signal in the low-pT region, and the effects of the trigger must be very small.
- drach09's blog
- Login or register to post comments
