- genevb's home page
- Posts
- 2024
- 2023
- 2022
- September (1)
- 2021
- 2020
- 2019
- 2018
- 2017
- December (1)
- October (3)
- September (1)
- August (1)
- July (2)
- June (2)
- April (2)
- March (2)
- February (1)
- 2016
- November (2)
- September (1)
- August (2)
- July (1)
- June (2)
- May (2)
- April (1)
- March (5)
- February (2)
- January (1)
- 2015
- December (1)
- October (1)
- September (2)
- June (1)
- May (2)
- April (2)
- March (3)
- February (1)
- January (3)
- 2014
- 2013
- 2012
- 2011
- January (3)
- 2010
- February (4)
- 2009
- 2008
- 2005
- October (1)
- My blog
- Post new blog entry
- All blogs
Another Look at Impacts of SpaceCharge and GridLeak
I ran a simple test of artificially adding SpaceCharge and GridLeak (in separate tests) to see the impact on pT and DCA using the track-by-track comparison tool (documentation You do not have access to view this node), with a modification to also look at primary tracks. (I had taken a very small look at impact on primary tracks in 2008, but it was not a thorough investigation.)
I. SpaceCharge
I modified StMagUtilities to add 0.01 to the TPC's SpaceCharge only when doing the distortion calculation in StMagUtilities::UndoSpaceChargeR2Distortion(), so that GridLeak wasn't impacted for this study.
I think looked at q*Δ(pT)/pT2 = -Δ(q/pT) [c/GeV] and Δ(sDCA) [cm] vs. various quantities. Note that primary tracks have no sDCA as they are forced to go through the primary vertex.
I begin with a Run 12 UU193 dataset:
What we see is that the primaries show a sinusoid, which is more indicative of change in the primary vertex position than a distortion-induced pT shift. This appears to be due to the clearly visible effect in the globals that some of the TPC sectors for this particular dataset are different from the other sectors. There is a group of sectors that are all in one region of phi (6,7,8,16) that are also missing their inner RDO, as seen in the below QA plots from the run examined (run 13115004). And because the inner-most padrows are the most distorted and are the most important for the track projection to the primary vertex, this region in phi has tracks whose projection to the primary vertex are altered the least, causing bias in the "de-focusing" of the primary vertex that SpaceCharge should induce.
So let's try again with a different dataset. I decided to go with some Run 14 AuAu data (run 15165004) that I found with no dead inner RDOs. Let's start with plots of the condition of the TPC:
...and here are the distortion impact plots...
Things are much more clear for the impacts of SpaceCharge now without the sine wave for primaries and the outlier sectors for globals. The below plots show the above two datasets' phi-integrated q*Δ(pT)/pT2 for globals (red) and primaries (black). The UU193 dataset on the left shows more smearing doing to the RDO outages, and the AuAu200 on the right has sharper peaks.
The next question to ask is how this pT shift changes with pT. Here's a plot of q*Δ(pT)/pT2 vs. q/pT (so high pT is towards the center) for the two datasets I examined (left: UU193, right: AuAu200) for globals (top) and primaries (bottom):
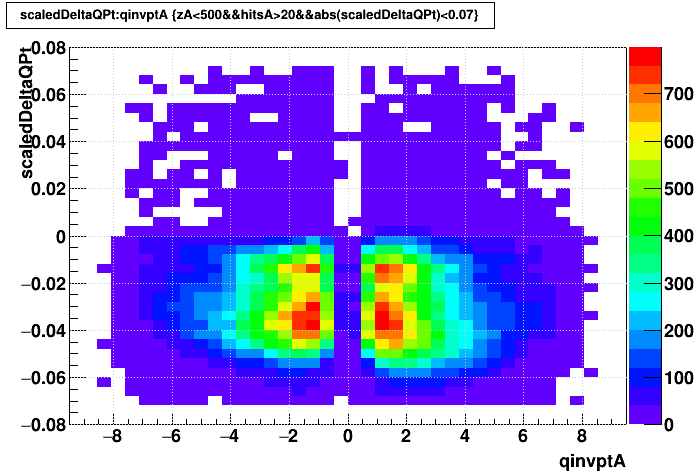
In general, SpaceCharge impacts don't show much pT dependence for global tracks, but there is some noticeable dependence for primary tracks. One tiny point that surprised me is that for global tracks, one can see that the shift is a little bit larger for q>0 (right half of the plot) than for q<0 (left half of the plot).
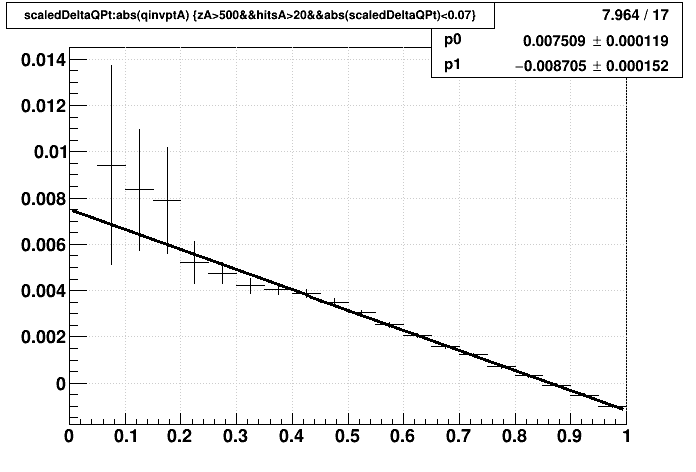
For the UU dataset, the profiles of these histograms for globals (red) and primaries (black) are shown on the left plot below, overlaid together along with sector 20's globals (blue) and primaries (green) also shown. An interesting observation is the asymmetry, seen most strikingly in primaries, at low pT, for q<0 vs. q>0. This is understood and is due to the fact that the distortion is a radial shift as well as an azimuthal shift. The azimuthal shift affects positive track pT) in one direction, while negative track pT) in the opposite direction, which is why the variable on the vertical axis is q/pT). However, the radial shift affects positive track pT) and negative track pT) in the same direction, which then shows up as an asymmetry in this observable. At high pT), the radial shift makes no difference because the track is radial and the shift is along the track, but at low pT this as an observable impact. The middle plot shows the full globals and primaries with the radial portion of the distortion flipped in direction, demonstrating that its impact on the asymmetry is flipped. Lastly, the plot on the right is a zoom-in and fit to the high pT behavior of primary tracks, indicating a Δ(q/pT) shift of 0.0075±0.0001 at infinite pT for SpaceCharge of 0.01, compared to (approximately) -0.033 for globals (a ratio of about -4.4:1 for globals to primaries at high pT).
Similarly, here's the Δ(sDCA) shift for globals (red) vs. q/pT, with sector 20 separated (blue):
II. GridLeak
I did a test next where I increased the GirdLeak distortion, separately from the SpaceCharge distortion. Using the same Run 14 AuAu200 dataset, I increased GL by 8.0, but this needs the context of SpaceCharge = 0.0218, so I'm actually increasing SC*GL by 0.174. Keep in mind that sectors 6 & 17 have no hits on padrows just outside the GridLeak region, while sector 20 has no hits just inside the GridLeak region. Here are the results:
The abnormal sectors don't seem to have a large impact on the overall picture. The below plots show the phi-integrated q*Δ(pT)/pT2 for globals (red) and primaries (black). These are much more broad peaks than they were for SpaceCharge.
Here are plots of q*Δ(pT)/pT2 vs. q/pT for globals (top) and primaries (bottom):
This shows a clear pT dependence for GridLeak perhaps going as pT3 instead of pT2, but primaries show much much less pT dependence. There is again the effect that q>0 low pT tracks show a larger impact than q<0, which is again certainly explained by the radial component of the distortion (not demonstrated here).
Below are profiles of those histograms for the globals (red) and primaries (black), with sector 20 separated for globals (blue) and primaries (green), making it clear that primary tracks are notably differently affected at high pT for sector 20 compared to the other sectors:
Similarly, here's the Δ(sDCA) shift for globals (red) vs. q/pT, with sector 20 separated out (blue):
-Gene
I. SpaceCharge
I modified StMagUtilities to add 0.01 to the TPC's SpaceCharge only when doing the distortion calculation in StMagUtilities::UndoSpaceChargeR2Distortion(), so that GridLeak wasn't impacted for this study.
I think looked at q*Δ(pT)/pT2 = -Δ(q/pT) [c/GeV] and Δ(sDCA) [cm] vs. various quantities. Note that primary tracks have no sDCA as they are forced to go through the primary vertex.
I begin with a Run 12 UU193 dataset:
| Run 12 UU193 | east | west |
|---|---|---|
| globals Δ(sDCA) |
 |
 |
| globals q*Δ(pT)/pT2 |
 |
 |
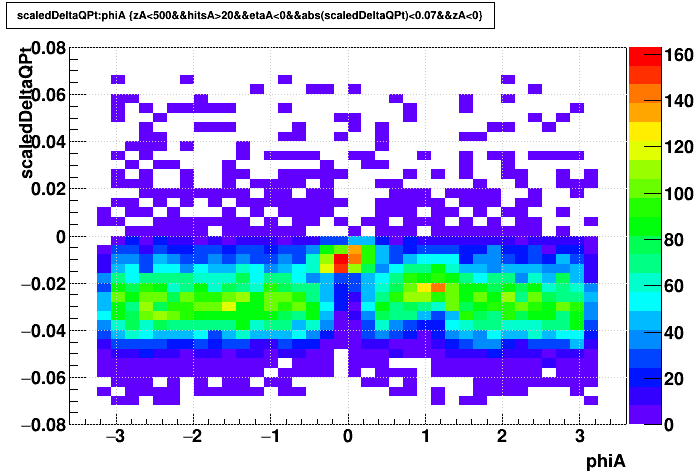| primaries q*Δ(pT)/pT2 |
 |
 |
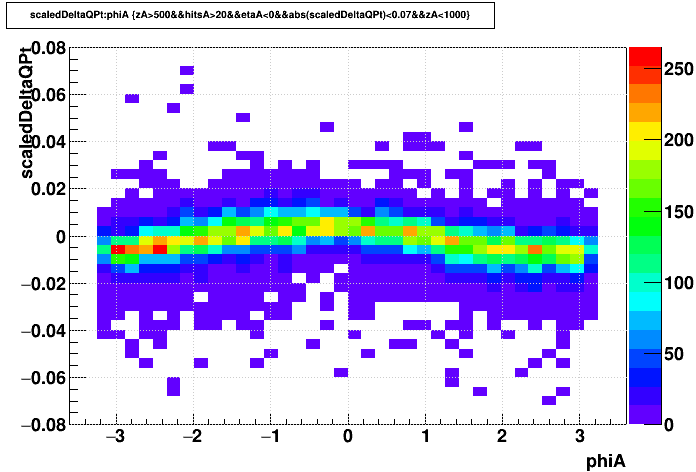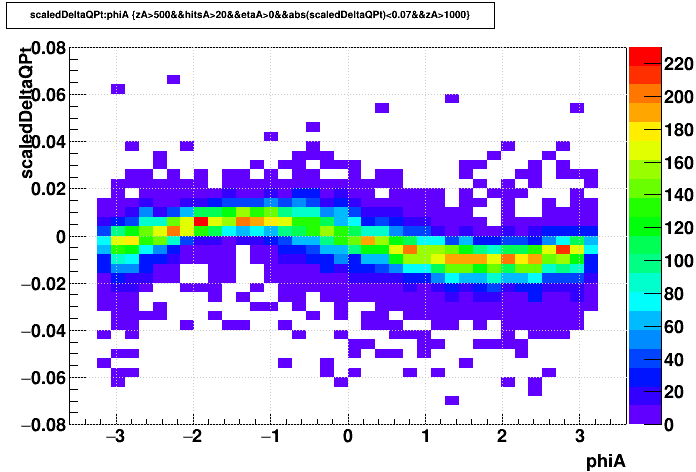What we see is that the primaries show a sinusoid, which is more indicative of change in the primary vertex position than a distortion-induced pT shift. This appears to be due to the clearly visible effect in the globals that some of the TPC sectors for this particular dataset are different from the other sectors. There is a group of sectors that are all in one region of phi (6,7,8,16) that are also missing their inner RDO, as seen in the below QA plots from the run examined (run 13115004). And because the inner-most padrows are the most distorted and are the most important for the track projection to the primary vertex, this region in phi has tracks whose projection to the primary vertex are altered the least, causing bias in the "de-focusing" of the primary vertex that SpaceCharge should induce.
| Sectors 1-12 (west TPC) | Sectors 13-24 (east TPC) |
 |
 |
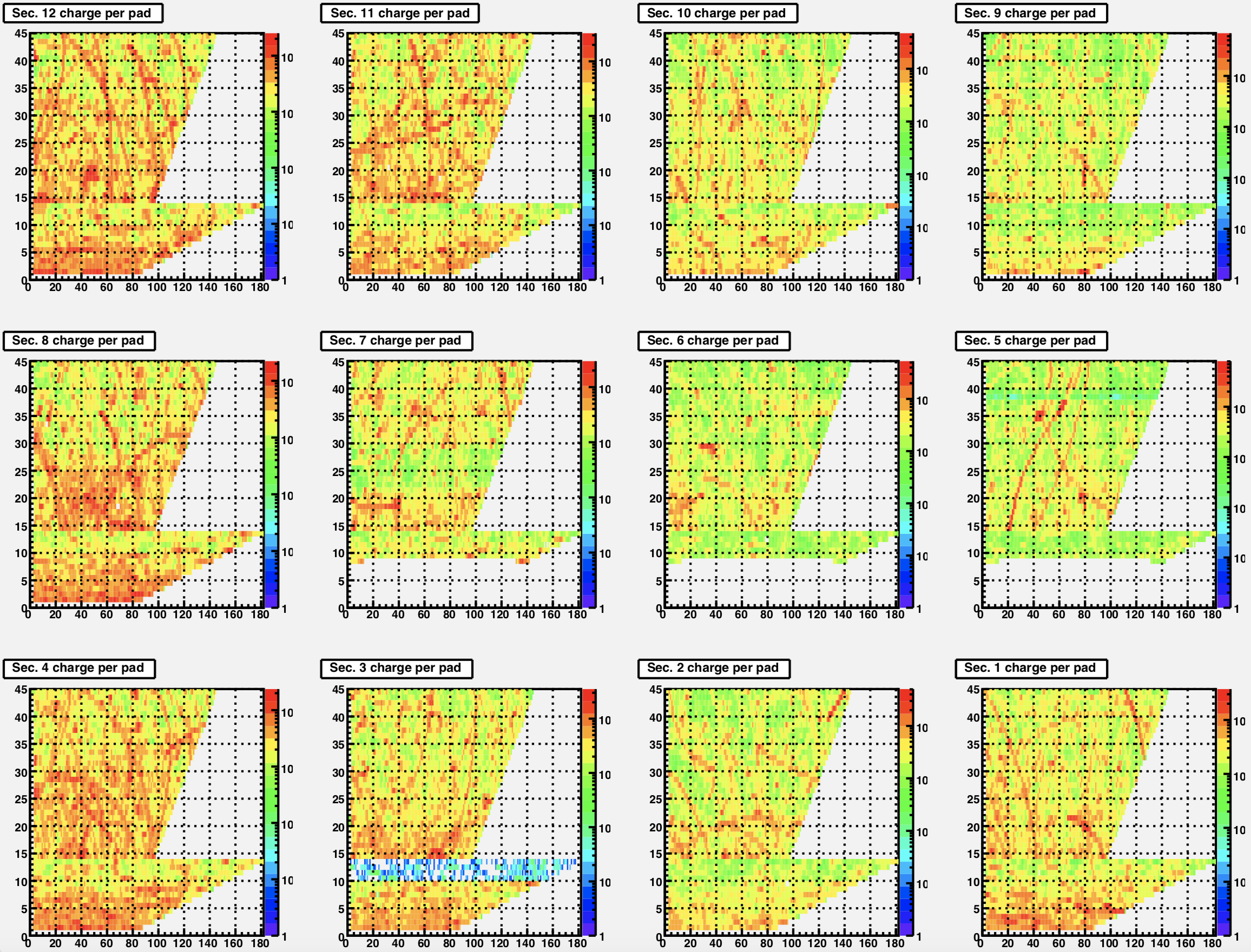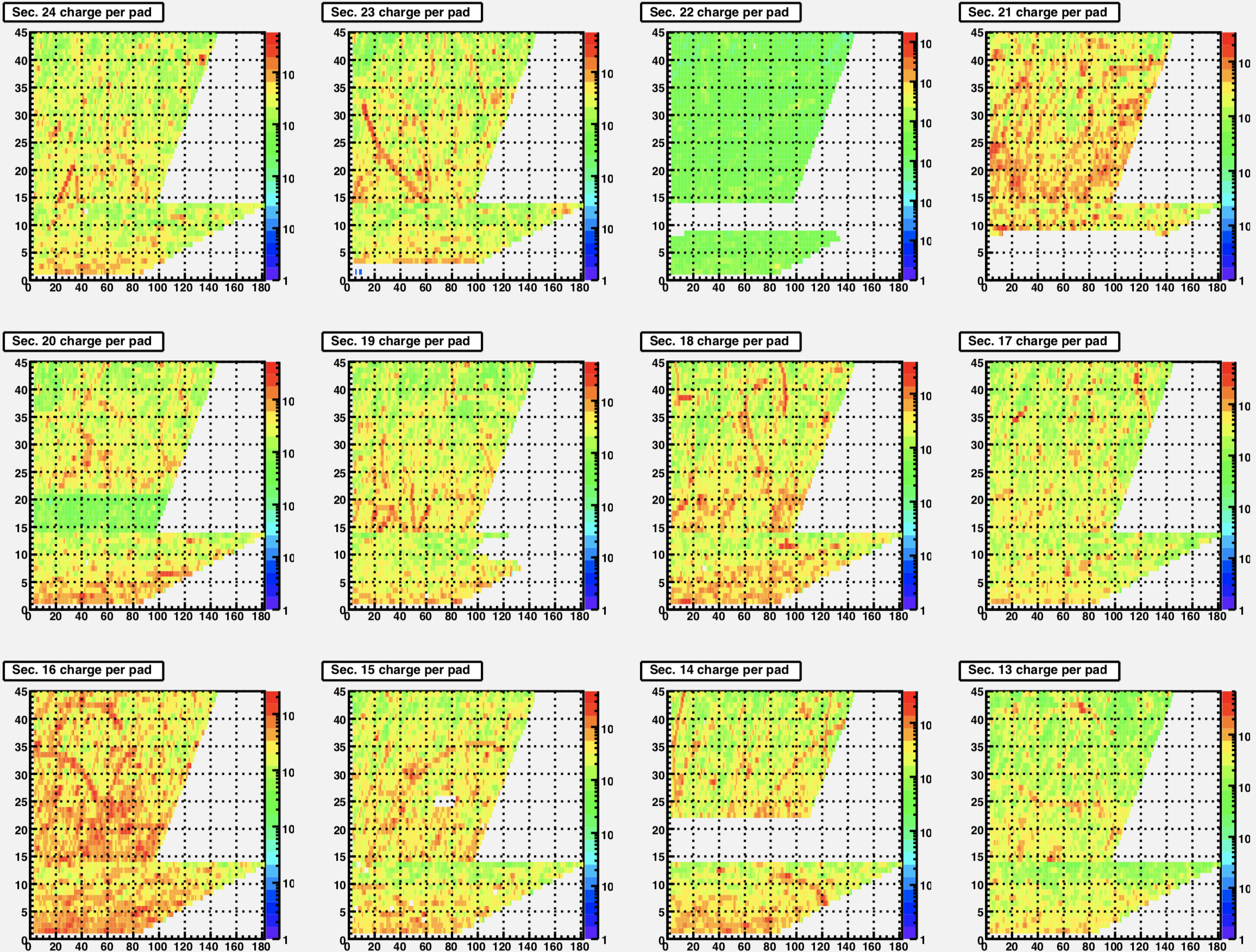So let's try again with a different dataset. I decided to go with some Run 14 AuAu data (run 15165004) that I found with no dead inner RDOs. Let's start with plots of the condition of the TPC:
| Sectors 1-12 (west TPC) | Sectors 13-24 (east TPC) |
 |
 |
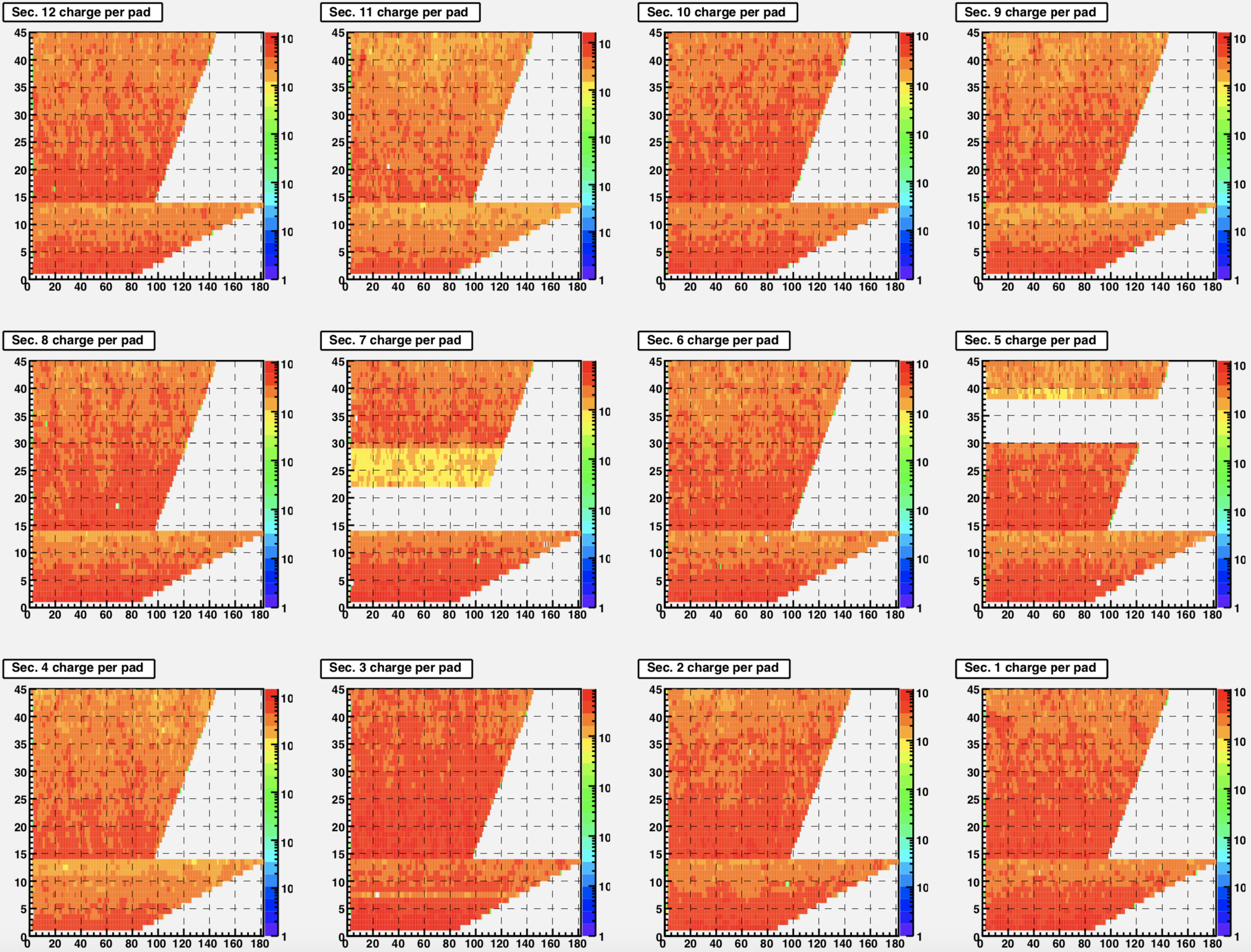...and here are the distortion impact plots...
| Run 14 AuAu200 | east | west |
|---|---|---|
| globals Δ(sDCA) |
 |
 |
| globals q*Δ(pT)/pT2 |
 |
 |
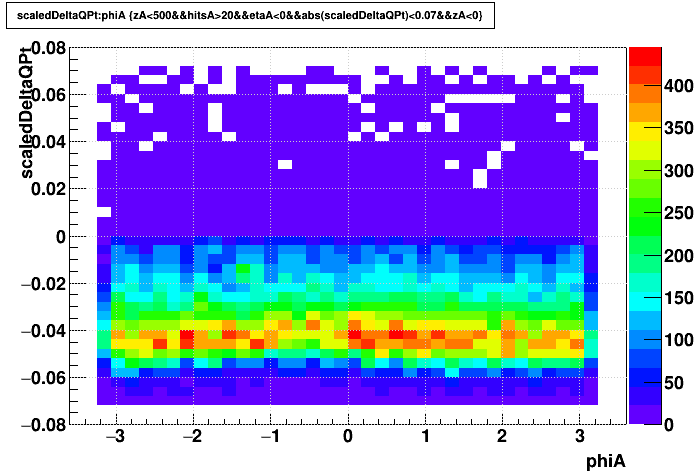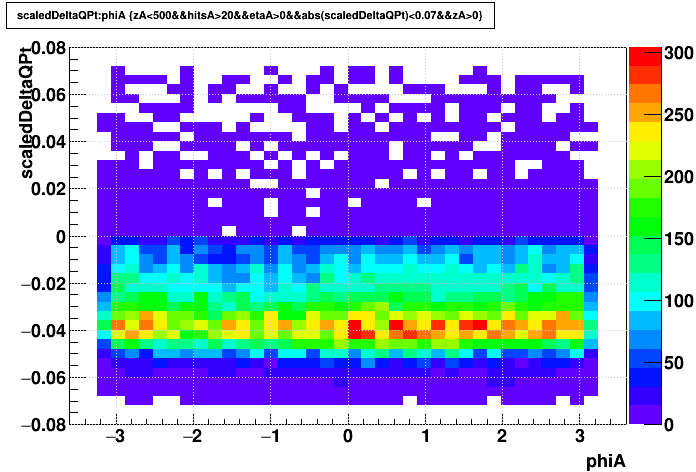| primaries q*Δ(pT)/pT2 |
 |
 |
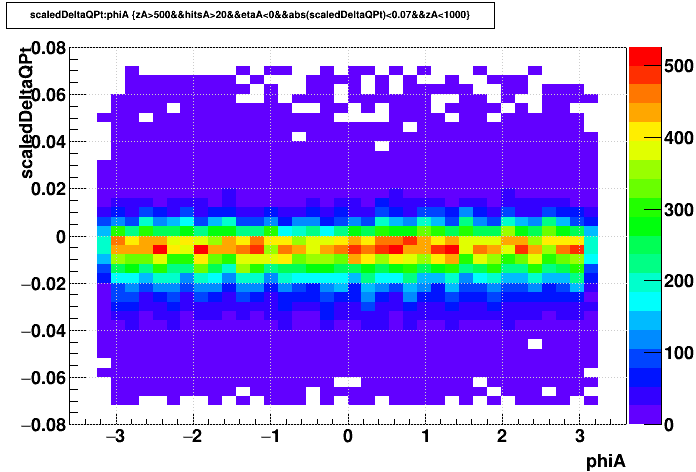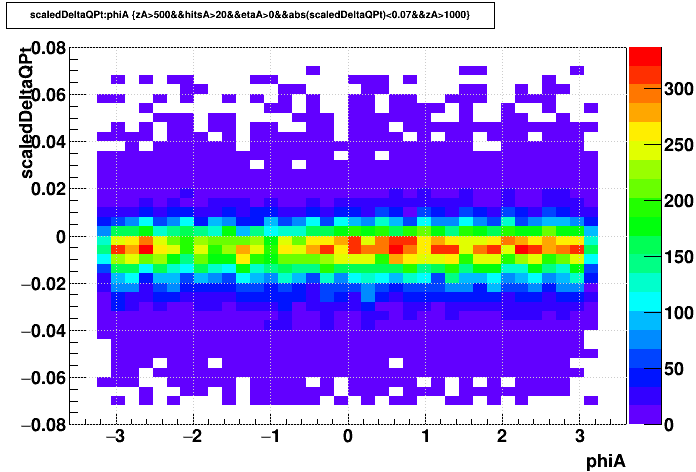Things are much more clear for the impacts of SpaceCharge now without the sine wave for primaries and the outlier sectors for globals. The below plots show the above two datasets' phi-integrated q*Δ(pT)/pT2 for globals (red) and primaries (black). The UU193 dataset on the left shows more smearing doing to the RDO outages, and the AuAu200 on the right has sharper peaks.
The next question to ask is how this pT shift changes with pT. Here's a plot of q*Δ(pT)/pT2 vs. q/pT (so high pT is towards the center) for the two datasets I examined (left: UU193, right: AuAu200) for globals (top) and primaries (bottom):
In general, SpaceCharge impacts don't show much pT dependence for global tracks, but there is some noticeable dependence for primary tracks. One tiny point that surprised me is that for global tracks, one can see that the shift is a little bit larger for q>0 (right half of the plot) than for q<0 (left half of the plot).
For the UU dataset, the profiles of these histograms for globals (red) and primaries (black) are shown on the left plot below, overlaid together along with sector 20's globals (blue) and primaries (green) also shown. An interesting observation is the asymmetry, seen most strikingly in primaries, at low pT, for q<0 vs. q>0. This is understood and is due to the fact that the distortion is a radial shift as well as an azimuthal shift. The azimuthal shift affects positive track pT) in one direction, while negative track pT) in the opposite direction, which is why the variable on the vertical axis is q/pT). However, the radial shift affects positive track pT) and negative track pT) in the same direction, which then shows up as an asymmetry in this observable. At high pT), the radial shift makes no difference because the track is radial and the shift is along the track, but at low pT this as an observable impact. The middle plot shows the full globals and primaries with the radial portion of the distortion flipped in direction, demonstrating that its impact on the asymmetry is flipped. Lastly, the plot on the right is a zoom-in and fit to the high pT behavior of primary tracks, indicating a Δ(q/pT) shift of 0.0075±0.0001 at infinite pT for SpaceCharge of 0.01, compared to (approximately) -0.033 for globals (a ratio of about -4.4:1 for globals to primaries at high pT).
Similarly, here's the Δ(sDCA) shift for globals (red) vs. q/pT, with sector 20 separated (blue):
II. GridLeak
I did a test next where I increased the GirdLeak distortion, separately from the SpaceCharge distortion. Using the same Run 14 AuAu200 dataset, I increased GL by 8.0, but this needs the context of SpaceCharge = 0.0218, so I'm actually increasing SC*GL by 0.174. Keep in mind that sectors 6 & 17 have no hits on padrows just outside the GridLeak region, while sector 20 has no hits just inside the GridLeak region. Here are the results:
| Run 14 AuAu200 | east | west |
|---|---|---|
| globals Δ(sDCA) |
 |
 |
| globals q*Δ(pT)/pT2 |
 |
 |
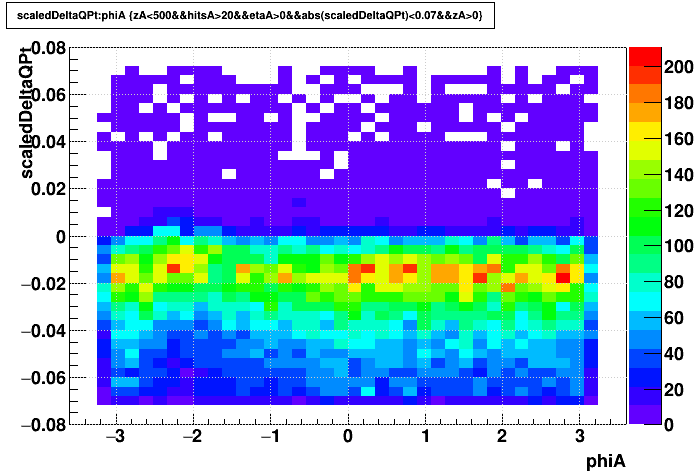| primaries q*Δ(pT)/pT2 |
 |
 |
The abnormal sectors don't seem to have a large impact on the overall picture. The below plots show the phi-integrated q*Δ(pT)/pT2 for globals (red) and primaries (black). These are much more broad peaks than they were for SpaceCharge.
Here are plots of q*Δ(pT)/pT2 vs. q/pT for globals (top) and primaries (bottom):
This shows a clear pT dependence for GridLeak perhaps going as pT3 instead of pT2, but primaries show much much less pT dependence. There is again the effect that q>0 low pT tracks show a larger impact than q<0, which is again certainly explained by the radial component of the distortion (not demonstrated here).
Below are profiles of those histograms for the globals (red) and primaries (black), with sector 20 separated for globals (blue) and primaries (green), making it clear that primary tracks are notably differently affected at high pT for sector 20 compared to the other sectors:
Similarly, here's the Δ(sDCA) shift for globals (red) vs. q/pT, with sector 20 separated out (blue):
-Gene
Groups:
- genevb's blog
- Login or register to post comments