gcc 4.3.2 compared to gcc 4.5
Tests
NIST Marks
I heard many statements on improvements or drop of compile code performance when moving from gcc 4.3.2 to gcc 4.5. It seems everyone is forgetting that a single blog with results is rather irrelevant to draw conclusions: performance increase / decrease is highly dependent on the kind of calculation your application performs as well as the optimization level and features used (vectorization, etc ...) and hence, a test suite is necessary to give a good indications.
I used a Spec mark test suite created by NIST called SciMark2. SciMark2 is composed of multiple tests as follows:
- Fast Fourier Transform - this test performs a one-dimensional forward transform of 4K complex numbers. The program starts with a bit-reversal portion (no flops) and the second performs the actual Nlog(N) computational steps. This exercises complex arithmetic, shuffling, non-constant memory references and trigonometric functions.
- Successive Over-relax - or a Jacobi Successive Over-relaxation test. The test exercises typical access patterns in finite difference applications, for example, solving Laplace's equation in 2D with Drichlet boundary conditions. The algorithm is tailored to measure basic "grid averaging" memory patterns, where each A(i,j) is assigned an average weighting of its four nearest neighbors.
- Monte-Carlo - is actually a Monte-Carlo integration test. It approximates the value of Pi by computing the integral of the quarter circle. The algorithm exercises random-number generators, synchronized function calls, and function inlining.
- Sparse matmult - the Sparse Matrix multiplication test uses an unstructured sparse matrix stored in compressed-row format with a prescribed sparsity structure. A 1,000 x 1,000 sparse matrix with 5,000 nonzeros is used. This exercises indirection addressing and non-regular memory references.
- Dense LU matrix - Dense LU matrix factorization computes the LU factorization of a dense 100x100 matrix using partial pivoting. Exercises linear algebra kernels (BLAS) and dense matrix operations.
A Composite test is computed to evaluate a typical average. BEWARE this average may NOT be relevant for your application as satted above. Also note before looking at the graphs below that function inlining kicks in only at -O3 (this may be relevant as there is an inline function bug in gcc 4.3.2 possibly forcing your application to be compiled with -fno-inline as reported in You do not have access to view this node. All tests were done 10 times and an average taken (this first wave was done using OO calc and I did not include the error bars which are marginal).
Several tests were performed summarized in the table below:
| 32 bits | 64 bits | |
| gcc 4.3.2 | 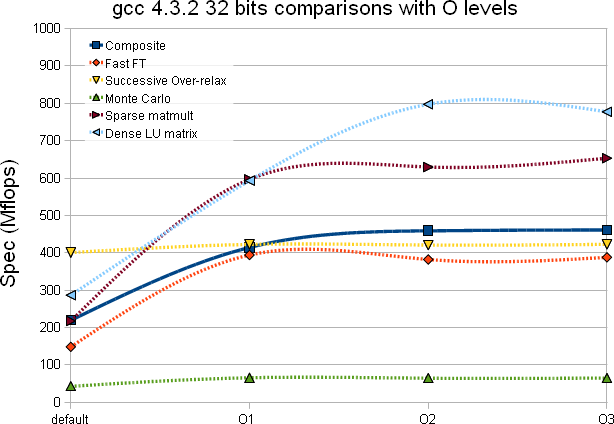 |
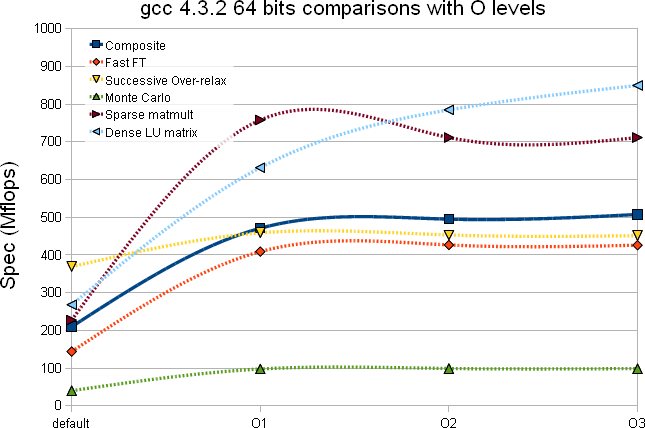 |
| gcc 4.5 | 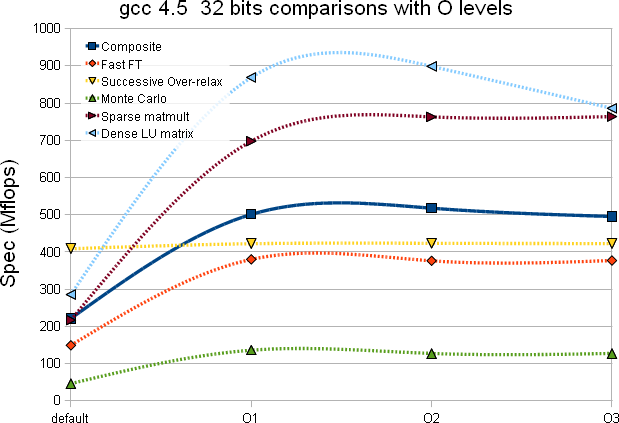 |
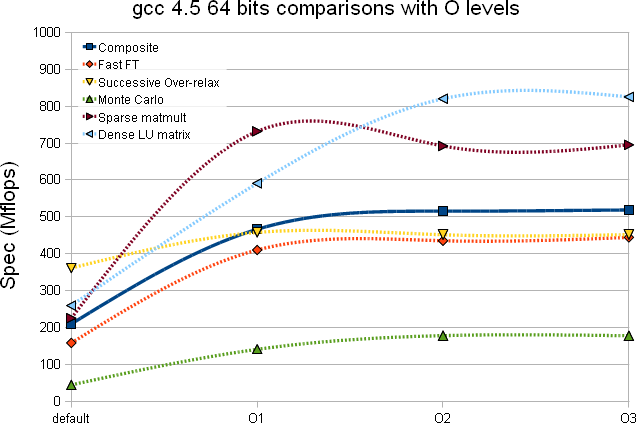 |
|
(vertical look) From 4.3.2 to 4.5 |
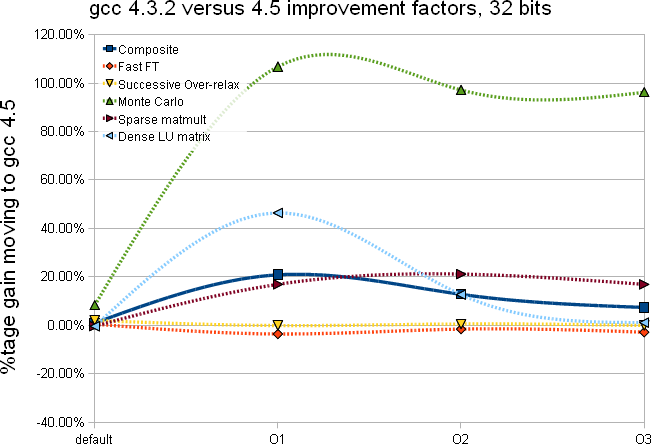 |
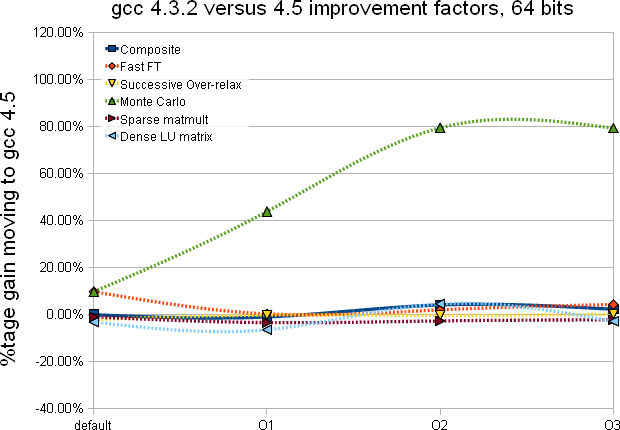 |
|
gcc 4.3.2, from 32->64 |
gcc 4.5, from 32->64 | |
|
(horizontal look) Going from 32 to 64 bits |
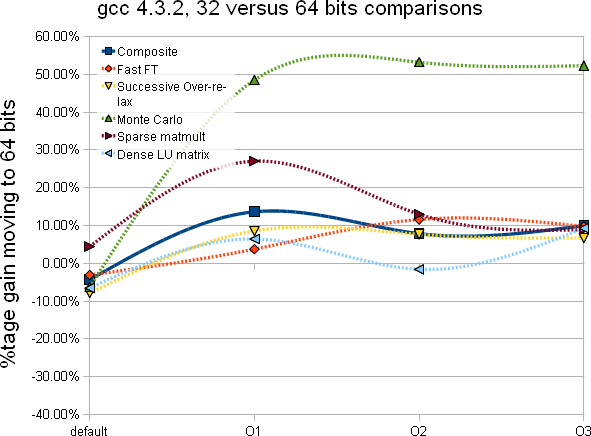 |
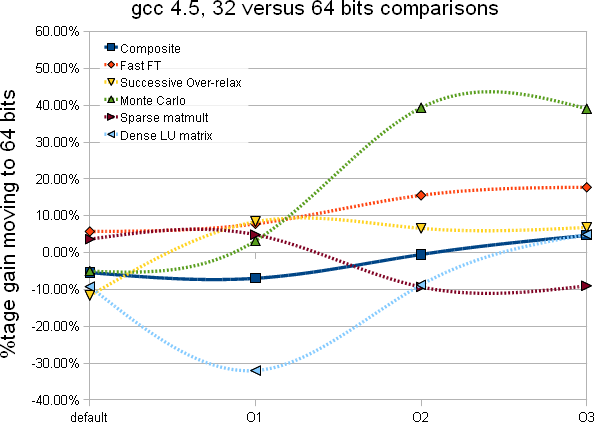 |
A few conclusions:
- First 4 graphs:
- There is a near consistency between the 32 and 64 bits and gcc 4.3.2 versus 4.5 when it comes to optimization level - beyond O2, there seem to be little to no improvements. gcc 4.5 may gives an overall Composite test with a net positive (the increase is subtle)
- The Dense LU matrix test is sensitive to the optimization level (improvement from the default compilation option to -O2 varies from 167% to 185%)
- The Monte-Carlo test is the second least subject to improvement based on the optimization level (the first was the SOR test) which is somewhat expected as the compiler can unlikely unroll, inline or play any other tricks
- With gcc 4.5 (Composite) it seems best to stop at -O2 optimization level (there is a slight drop at -O3 likely within error bars but since compilation takes that much longer and no gain is foreseen ...)
- From the bottom two graphs:
- Moving to 64 bits executable would cause a large gain for Monte-Carlo calculations (50% gain) and for algorithm alike Sparese matmult (i.e. memory referencing). This is good news as our code may be dominated by such calculations.
- Since our STAR code (optimized) are compiled with -O2, and if we believe the Composite test, the gain would be marginal and around 10%.
- With gcc 4.5, there is an inexplicabledrop of performance going to 64 bits compiled code. A hint we should stick to 32 bits compiled code in gcc 4.5 mode.
- The before last two graphs represents the gains moving from gcc 4.3.2 to gcc 4.5
- In both 32 and 64 bits mode, there is a gain varrying from 15% to 100%
- The biggest gain is on MonteCarlo calculations (could be up to 100% with -O2)
- Moving to 64 bits, we would gain nearly nothing (Composite) and up to 80% speed up on MonteCarlo like calulcations
ROOT Marks
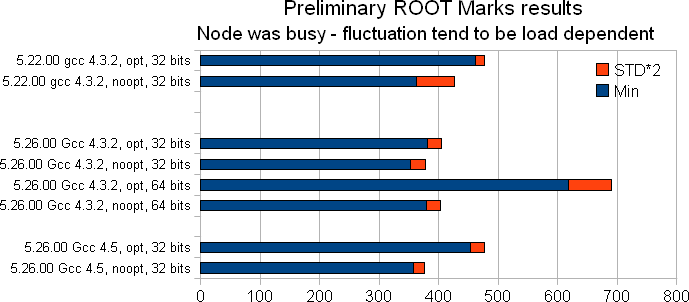
The gain in optimized mode for moving from gcc 4.3.2 to gcc 4.5 would be ~ 20% in this test. The marks would need to be redone (the standard deviation was rather large due to load).
root4star
(coming soon)
- jeromel's blog
- Login or register to post comments
