I've had a lot of trouble stabilizing the fit with the two-gaussian beam profile (narrow gaussian + wide gaussian), so I've moved to something simpler - assuming a two-gaussian vernier scan profile.  When you assume a two-gaussian beam profile, your overlap integral includes three terms, and to be properly normalized, there is a lot of interdependence on the fit parameters.  When you assume a two-gaussian vernier scan profile, there is no cross term, and the interdependence goes away.  Unfortunately, so does the strict correspondence between the fit and the values we want to extract.

In particular, we wish to extract the normalization and the width of the best-fit single gaussian to the double gaussian that best fits the vernier scan:

A*exp(-x^2/a^2)~B*exp(-x^2/b^2)+C*exp(-x^2/c^2)

Since we care about the validity of the fit near x=0 (where most of the overlap is), it seems reasonable to match terms as best we can about this point.  setting x=0 we get:

A=B+C,

and setting x=0 in the derivative gives us:

a^2=Ab^2c^2/(Bc^2+Cb^2)

With this in hand, I performed the fit and extracted B,b,C,c, and a flat background rate (which agrees with the value for that measured previously).

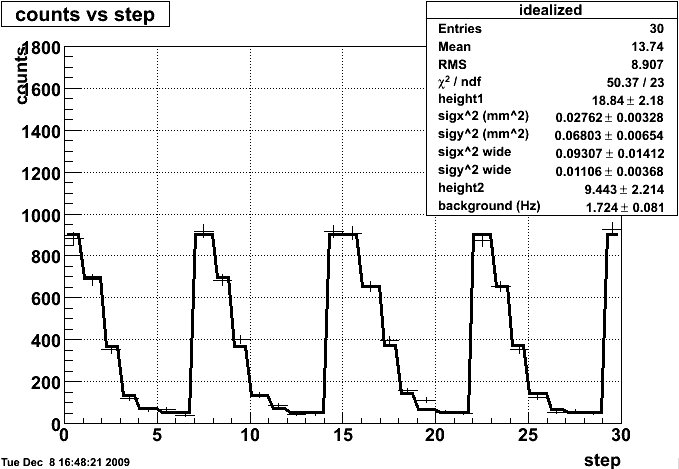
figure 1, the vernier scan fit for the first vernier scan run.  Note that unlike previous fits, we no longer systematically under-estimate the peak.

After using the relations above, and various constants for the run, this yields:

Cross section=342.084259nb

sx2=0.018049mm^2

sy2=0.012508mm^2

The cross section is considerably smaller than we've seen previously, but the gaussian widths are comparable.