Current EEMC pi0 reconstruction efficiency and comparision with Weihong's thesis.

Weihong's Estimates

Weihong's thesis (Section 4.4) has estimates of the reconstruction efficiency with three samples:

1. 10k events of two pi0s, flat in eta [1.1,1.9], phi [20,40] degrees, E [5,60] GeV.
2. 1k events of single pi0s, flat in eta [1.1,1.9], phi [-180,180] degrees, E [5,60] GeV.
3. 200k Pythia events, only using partonic pT bin 25-35 (unclear if 200k is all partonic pT bins or just this one)

At the time, all of the simulation had iron instead of air in some locations in the geometry.  Weihong states he applied a Delta R cut of 0.02 to associate generated and reconstructed pi0s.  Some of the code has a value of 0.04 in it, so it is currently unclear which value was used.  My code is currently using the value of Delta R = 0.04.

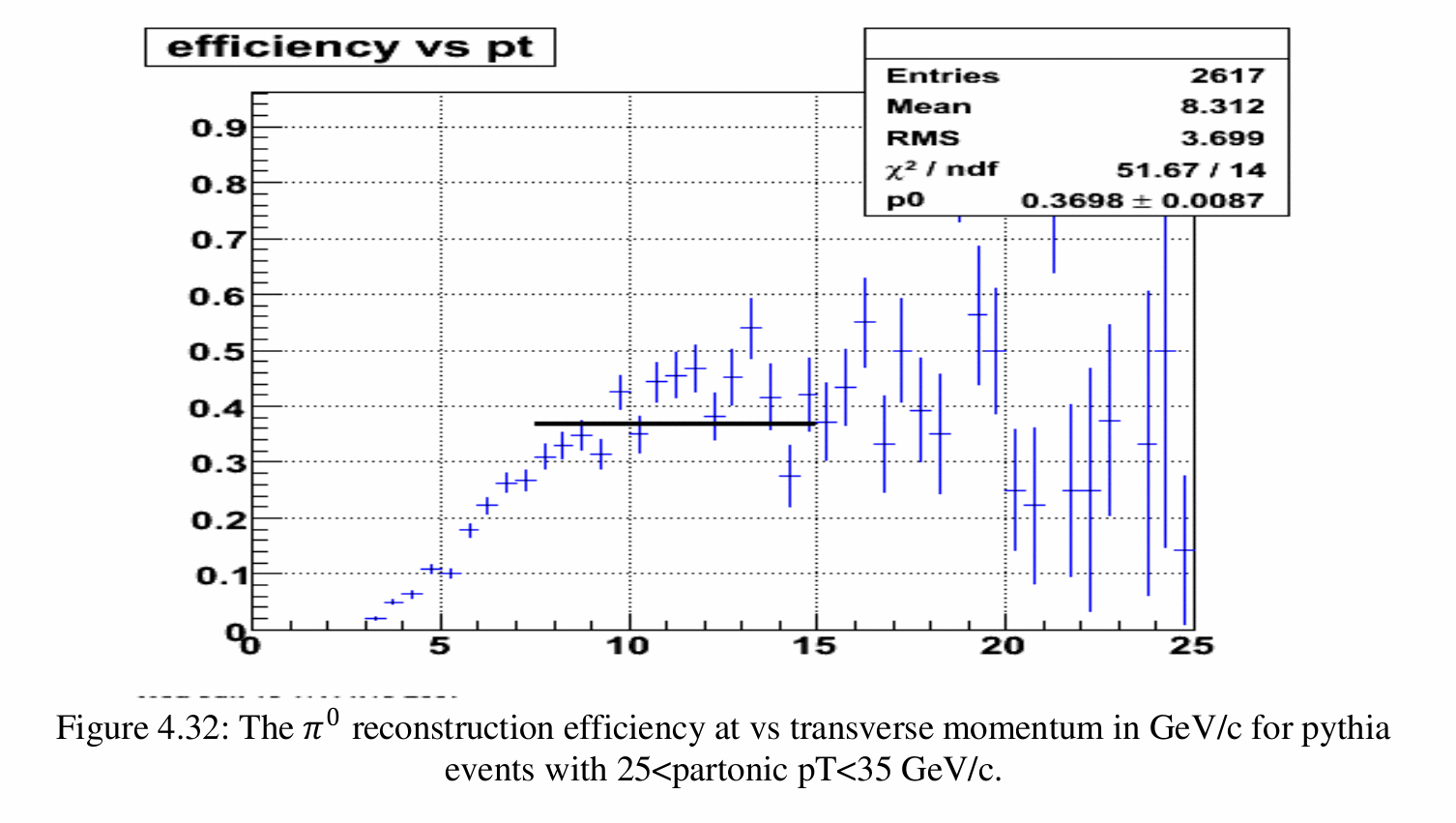
Weihong's estimates did not include any of the reconstruction cuts, and so the values are higher than the values using the cuts, needed for estimating the cross section.  Additionally, Weihong did not correct for the case when multiple reconstructed pi0s are near the same generated pi0.  This will also make his reconstrution efficiency appear higher than the actual value.  Additionally, he did not use the trigger emulator, which would cause his efficiecies to be lower than expected, as they include a combination of trigger (within filter) and reconstrution efficiencies.  The following plot shows his results for the Pythia sample.  The fit appears to be from about 7.5 to 15 GeV, and results in a value of 0.37.  The results for the efficiency using the other two samples were higher, but are less like the actualy setting of the data.

Newest Reconstruction Efficiency

The newest calculation is the reconstruction efficiency given events with the trigger, and include all Pythia partonic pT bins (about 1M events) and all cuts that the data have.  Also, the case of multiple reconstructed pi0s near a single generated pi0 is handled such as to not effect the reconstruction efficiency.  The following plots and figures also use the TSIU SMD clustering algorithm, instead of the IU SMD clustering algorithm.

 Before showing the final efficiencies, it is worthwhile to compare an intermediate value, which has everything in place except the cut on the pi0 invarient mass peak.  Among all of the cuts, this cut is the one that has the most effect on the reconstruction efficiency (by almost full order of magnitude).  The following plot is the smearing matrix, normalized per generated pi0 pT bin.  However, one minus the far right column gives the reconstruction efficiency.  The uncertainty is an order of magnitude smaller than the least significant digit. Note: the following is TSIU SMD clustering algorithm.

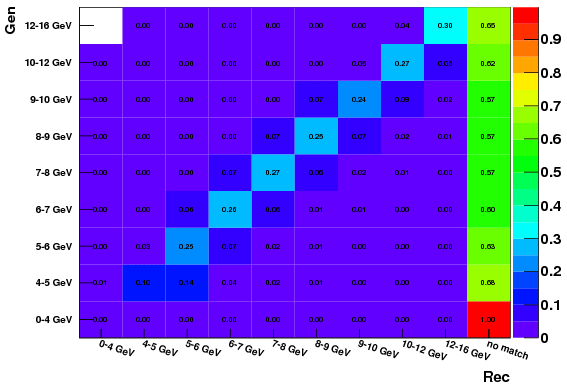
The recostruction efficiency is on the order of 0.43, which is comparable with Weihong's 0.37, given the many differences between the calculations (iron/air, cuts, triggers, split-treatment, etc.).  If I instead require the same pi0 mass peak window as in data (Mgg in 0.1 to 0.2 GeV), the following values are obtained:

Now the reconstruction efficiency has dropped to 0.28 in the mid-pT bins.  To show the dominant effect is not the different SMD clustering algorithm, the next figure is the same smearing matrix, but using the IU SMD clustering algorithm.

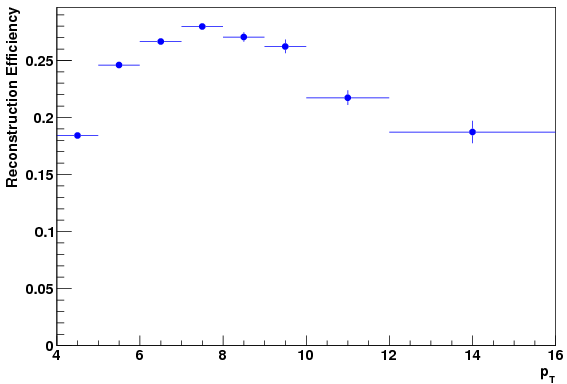
The final reconstruction efficiency incorperates the effect of smearing into the 0-4 GeV bin, and so shows slight differences than the above.  The actual numbers used to compute the cross section, as of now, are given in the following plot.  Note, the MC statistics are sufficient to provide a very small uncertainty on the values (smaller than the marker for the lower pT bins).  Also note, following plot is back to the TSIU SMD clustering algorithm.