2007.02.19 Summary of Reconstructed/Monte Carlo Photon Energy

 

Summary of Reconstructed/Monte Carlo Photon Energy

 

Description

The study presented here uses Monte Carlo data sets generated by Will Jacobs at different photon energies (5, 10, 20, 40, 80, 160 GeV):

• 10k photons
• vertex at 0
• eta 0.8-2.2
• SVT/SSD out

For each photon energy, the ratio E_reco/E_MC vs. eta was plotted and fitted to the function p0+p1*(1-eta), where E_reco is the reconstructed photon energy integrated over the

entire

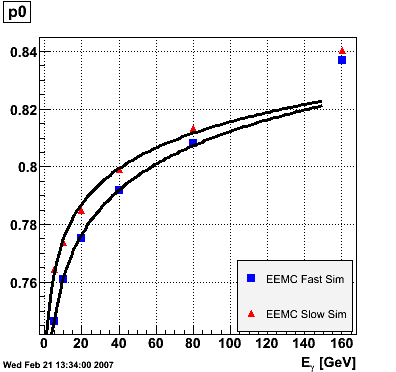
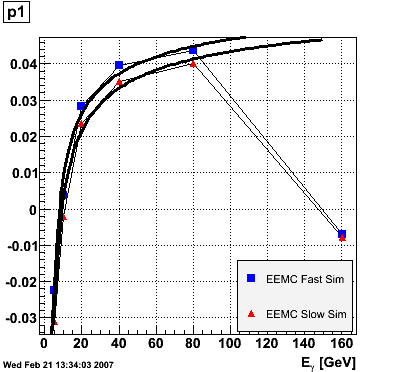
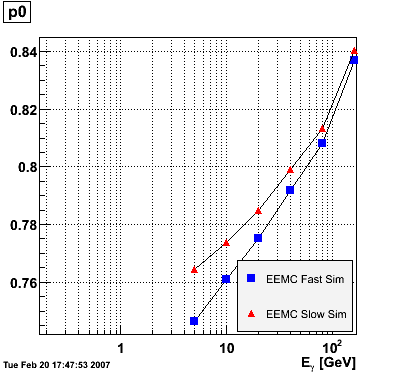
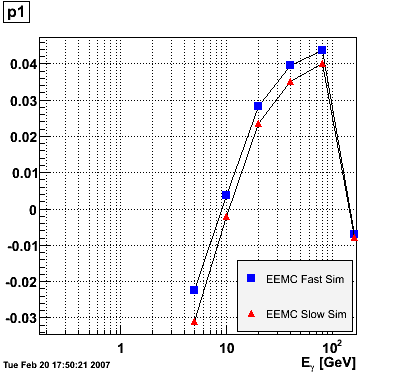
EEMC. The range of the fit was fixed from 1.15 to 1.95 to avoid EEMC edge effects. The advantage of parametrizing the eta-dependence of the ratio in this way is that p0 is immediately interpretable as the ratio in the middle of the EEMC. The parameters p0 and p1 vs. photon energy were subsequently plotted for the EEMC fast and slow simulator.

EEMC Fast/Slow Simulator Results

Conclusions

The parameter p0, i.e. the ratio E_reco/E_MC in the mid-region of the EEMC, increases monotonically from 0.74 at 5 GeV to 0.82 at 160 GeV, and the parameter p1, i.e. the slope of the eta-dependence, also increases monotonically from -0.035 at 5 GeV to 0.038 at 160 GeV. There appears to be a magic energy around 10 GeV where the response of the EEMC is nearly flat across its entire pseudorapidity range. The anomalous slope p1 at 160 GeV for the EEMC slow simulator is an EEMC hardware saturation effect. The EEMC uses 12-bit ADC's for reading out tower transverse energies and is set for a 60 GeV range. Any particle which deposits more than 60 GeV in E_T will be registered as depositing only 60 GeV as the ADC will return the maximum value of 4095. This translates into a limit on the eta range of the EEMC for a particular energy. Let's say that energy is 160 GeV and the EEMC tops at 60 GeV in E_T, then the minimum eta is acosh(160/60)=1.6. This limitation is noticeable in a plot of E_reco/E_MC vs. eta. This anomaly is not observed in the result of the EEMC fast simulator because the saturation behavior was not implemented at the time of the simulation (it has since been corrected). The energy-dependence of the parameter p0 is fitted to p0(E)=a+b*log(E) and the parameter p1 to p1(E)=a+b/log(E). The results are summarized below:

EEMC fast simulator fit p0(E)=a+b*log(E)
a = 0.709946 +/- 0.00157992
b = 0.022222 +/- 0.000501239

EEMC slow simulator fit p0(E)=a+b*log(E)
a = 0.733895 +/- 0.00359237
b = 0.0177537 +/- 0.0011397

EEMC fast simulator fit p1(E)=a+b/log(E)
a = 0.0849103 +/- 0.00556979
b = -0.175776 +/- 0.0138241

EEMC slow simulator fit p1(E)=a+b/log(E)
a = 0.0841488 +/- 0.0052557
b = -0.187769 +/- 0.0130445

---

Pibero Djawotho

Last updated Mon Feb 19 23:18:44 EST 2007