Previously, we had realized we weren't handling the jet-matching in the best manner.  The new (and old) matching algorithms are described in this post:

https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-06052018-run-9-embedding-new-matching-algorithm

This took care of the population of jets at high 'pTdetector' but low 'pTparticle'.  However, it also produced a large of population of jets with nonzero 'pTparticle' but with apparently zero 'pTdetector':

This was a bug in the code: the algorithm has a flag which indicates whether or not a match was found for a given particle jet, and a set of variables which keep track of the information of the "best" match for that particle jet.  The code won't update these match variables unless the candidate is "better" (i.e. has a 'qT' closer to one) than the current values.  Hence, there were situations where a match would be found, but it wasn't "better."  And so the response matrix would be filled with the particle jet 'pT' and the default match values (e.g. 'pTmatch = 0').

Now the match variables are all initialized to values which are definitely "worse" than any actual candidate.  The resultant response matrix is as so:

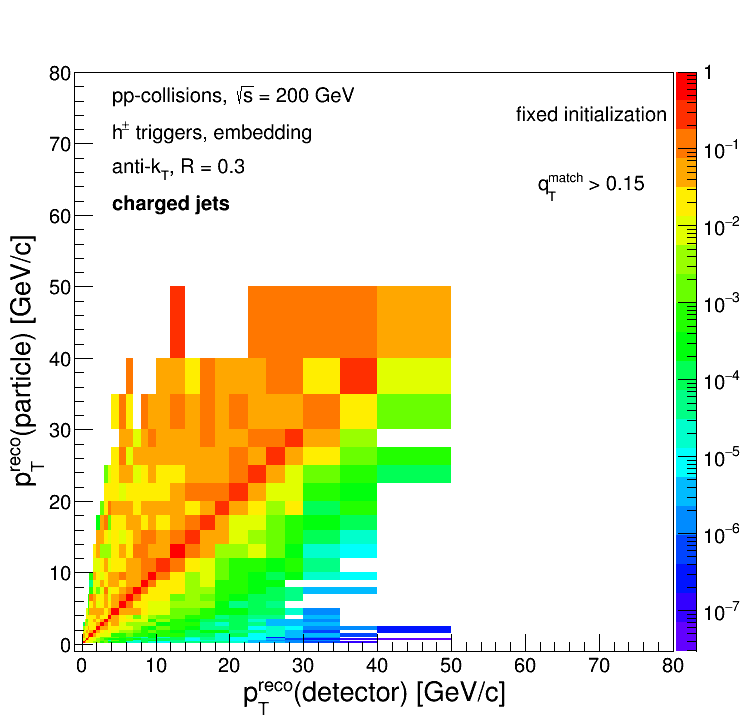
The old issue is back: we have odd situations where the matched 'pTdetector' is high, but the 'pTparticle' is low.  These correspond to situations where 'qT' is large; if there are no "better" candidates, then the response matrix will get filled with the match with the large 'qT'.  Here are the 'qT' distributions as a function of partonic 'pT' for the RFF configuration:

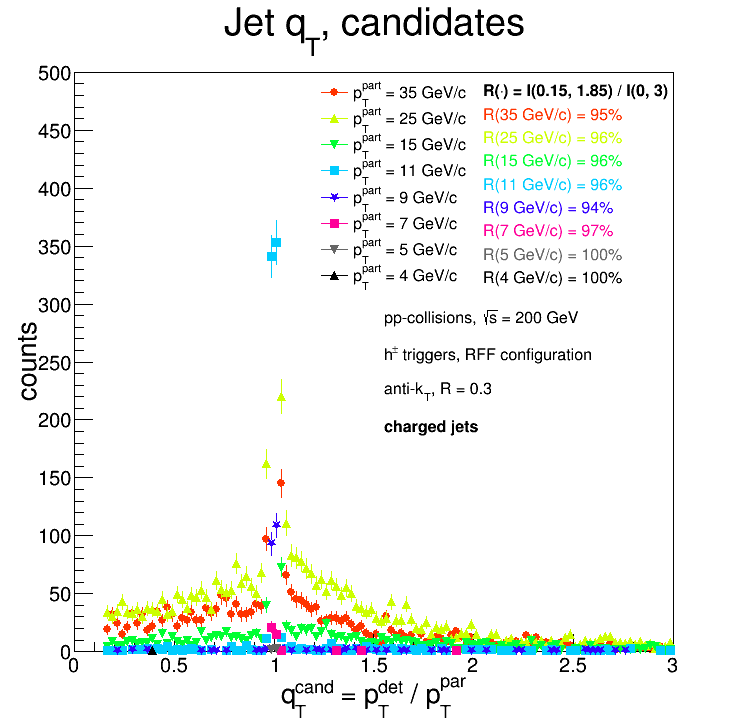
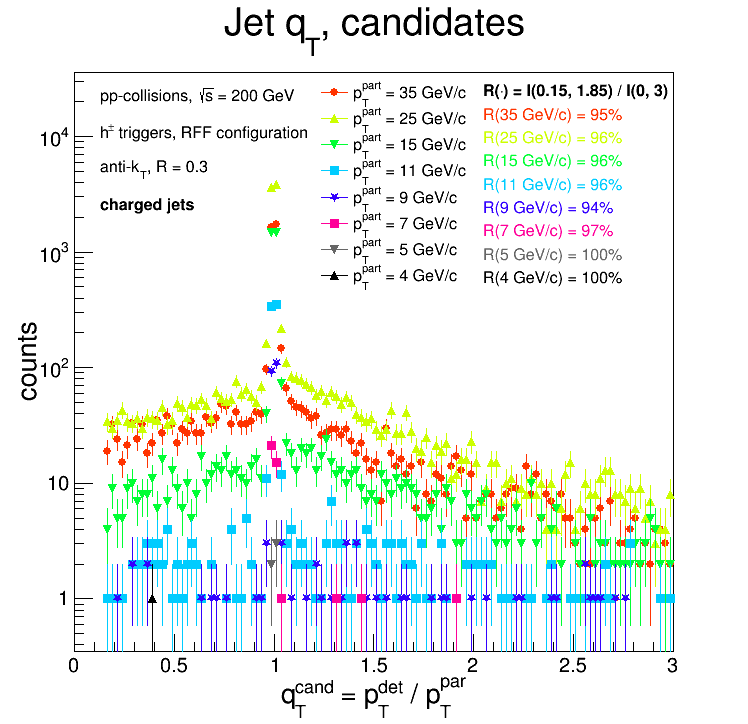
The listed percentages given the percentage of match candidates which fall between 'qT = 0.15' and 'qT = 1.85' (the amount candidates which have 'qT > 3.' is around 2% of the total no. of candidates).  The upper limit was chosen somewhat arbitrarily: since the lower limit is '0.15 = 1 - 0.85', I figured an upper limit of '1.85 = 1 + 0.85' would be nice and symmetric.  Applying this cut in the matching algorithm yields this response matrix:

Which looks fairly reasonable to me.  As usual, the relevant ROOT files are attached in a zip file.

Update [06.28.2018]: just for clarification, the matching here was done requiring a trigger to be present at the detector level and at the particle level, and was done with 'dR' defined to be 'dR = sqrt((dPhiMatch - dPhiTruth)^2 + (etaMatch - etaTruth)^2)' where 'dPhiMatch = phiMatch - phiTrgDet' and 'dPhiTruth = phiTruth - phiTrgPar' and are confined to the interval (-pi/2, 3pi/2).  Here 'phiTrgPar' and 'phiTrgDet' indicate the phi of the trigger at the particle and detector level respectively.