This is a continuation of this post:

https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-07012019-run-9-pp-unfolding-after-various-fixes

Now it is time to directly compare the two unfolding solutions (our pi0 data) from the previous post.  After ensuring that our parameterized response matches (at least reasonably well) with the response extracted from embedding, it shouldn't matter (much) if we unfold our data with the parameterized response or the embedding response.  The two solutions should be the same.

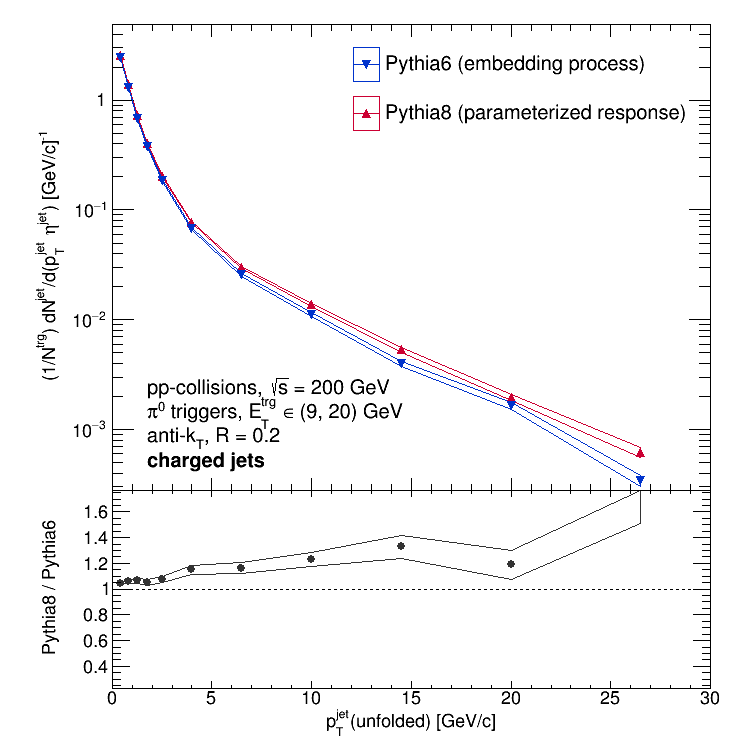
And they aren't...  The Pythia8 (parameterized response) solution is significantly harder than the Pythia6 (embedding response) solution.  My first thought was that it might be that the Pythia8 spectrum (both particle and detector level) is harder than the Pythia6 spectrum.  If that were the case, then it would be reasonable to expect that resultant solution is harder.  So is that the case?  First, here are the Pythia8 and Pythia6 priors (the particle-level spectra):

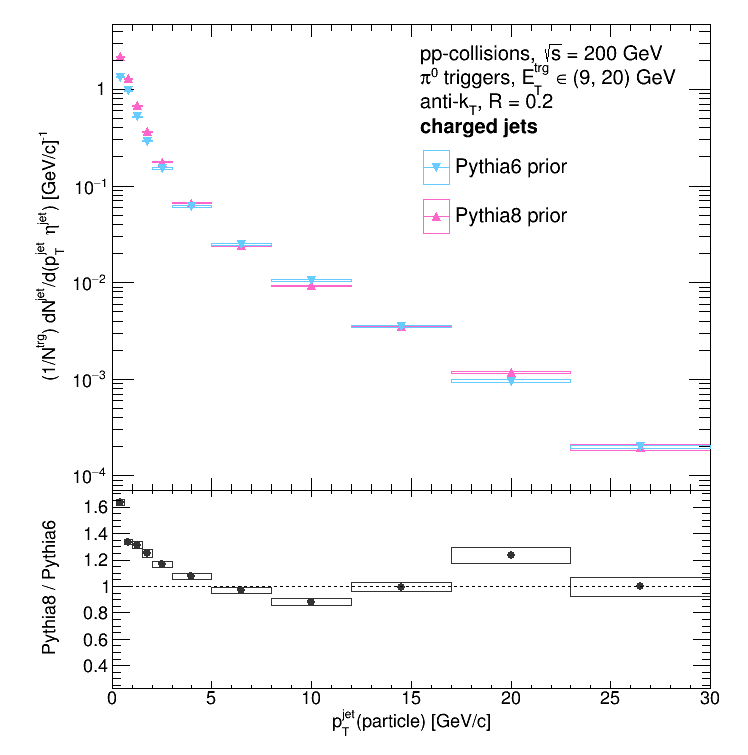
Hmmm... Next is the "smeared prior" -- the detector-level spectra.  Note that these spectra consist of all the detector-level jets that were successfully matched to particle-level jets.

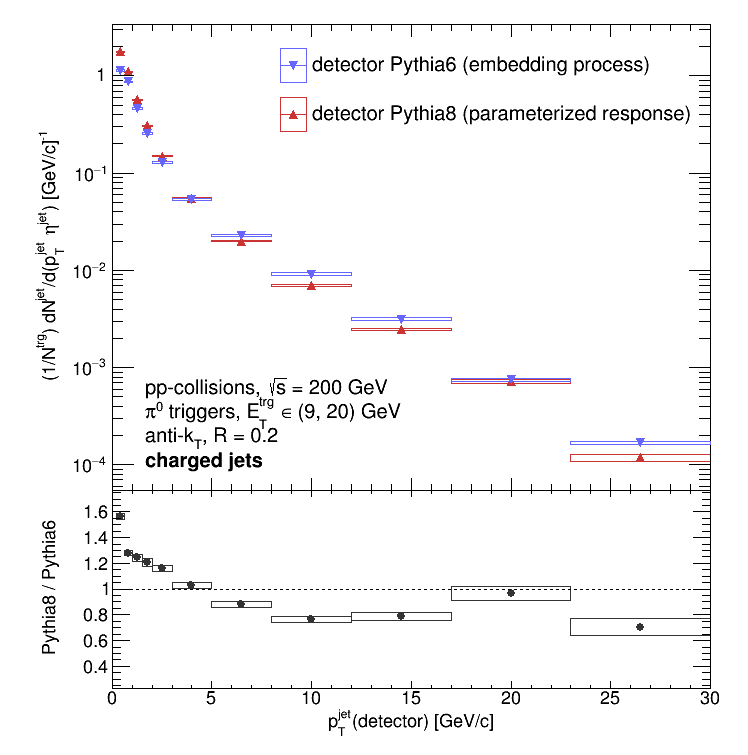
Oh dear.  It definitely does not seem to be the case that the Pythia8 spectra are harder than the Pythia6 spectra...  Here are all 3 combinations (prior, "smeared" prior, and unfolding solutions) on top of each other:

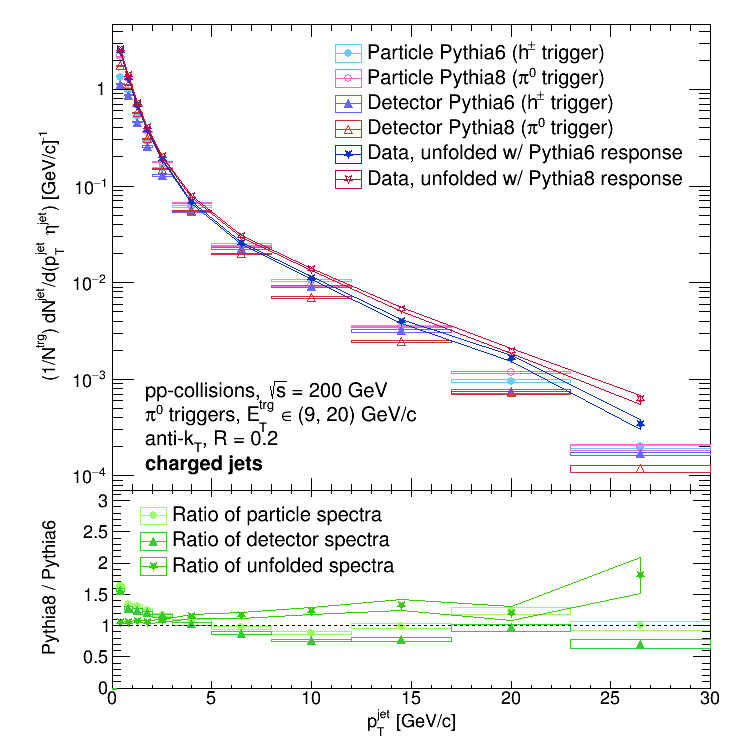
So the unfolding solutions' ratio trends the opposite direction of the priors' and smeared priors' ratios!  This is quite alarming!  Why should this be so?

To zeroth order, the correction factors applied to the data should go something like the ratio of the prior (particle level) spectrum to the smeared prior (detector level) spectrum.  We'll call these factors delta in the proceeding arguments.  It would follow then, since the data to be unfolded are the same between the two scenarios, that the delta's for Pythia8 should be larger than the delta's for Pythia6.  They should follow (roughly) the same trend as the unfolding solutions do.  To summarize:

1. delta = (particle level) / (detector level)
2. unfolded ~ data * delta
3. delta[Pythia8] / delta[Pythia6] = unfolded[Pythia8] / unfolded[Pythia6]

Is this so?

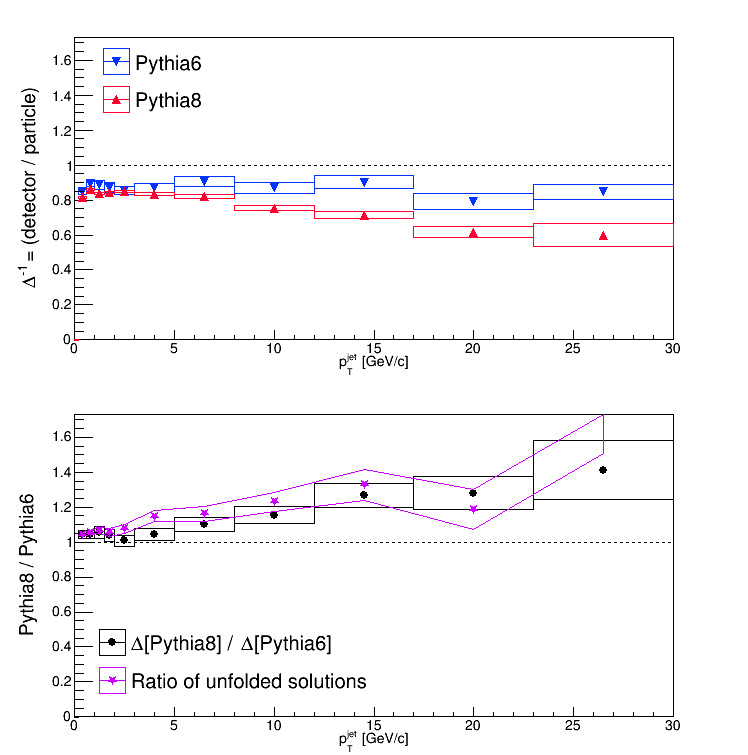
It is!  Previously, I had shown that the jet-finding efficiencies between the two responses matched sufficiently well:

https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-06252019-run-9-pp-pythia8-vs-pythia6-jet-matching-efficiency-after-fixes

So some thing else other than the parameterization of the response is going awry.  And the above argument suggests, to me, that there's an issue in the jet matching algorithm...  So next I will be diving into that.