Update 08.02.2018 -- Run 9 pp: Follow-Up On Weird SVD Behavior
Previously, I noted some "weird" behavior when I tried unfolding my distributions with the SVD algorithm:
https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-07262018-run-9-pp-weird-svd-behavior
I had assumed that the regularization parameter (k) should end up about the same magnitude as the one used in the Bayesian Algorithm despite that it means something different between the two algorithms. After reading some more into the RooUnfold documentation, there is no reason why this should be the case.
http://hepunx.rl.ac.uk/~adye/software/unfold/RooUnfold.html
To quote the manual on Bayesian unfolding:
"For RooUnfoldBayes, the regularization parameter specifies the number of iterations, starting with the training sample truth (iterations = 0). You should choose a small integer greater than 0 (we use 4 in the examples). Since only a few iterations are needed, a reasonable performance can usually be obtained without fine-tuning the parameter. The optimal regularization parameter can be selected by finding the largest value up to which the errors remain reasonable (i.e. do not become much larger than previous values). This will give the smallest systematic errors (reconstructed distribution least biased by the training truth), without too-large statistical errors. Since the statistical errors grow quite rapidly beyond this point, but the systematic bias changes quite slowly below it, it can be prudent to reduce the regularization parameter a little below this optimal point."
So far, k = 2 or 3 has usually been ideal when using Bayes. However, the manual has this to say about SVD unfolding:
"For RooUnfoldSvd, the unfolding is something like a Fourier expansion in 'result to be obtained' vs. 'MC truth input'. Low frequencies are assumed to be systematic differences between the training MC and the data, which should be retained in the output. High frequencies are assumed to arise from statistical fluctuations in data and unfortunately get numerically enhanced without proper regularization. Choosing the regularization parameter, k, effectively determines up to which frequencies the terms in the expansion are kept. (Actually, this is not quite true, we don't use a hard cut-off but a smooth one.)
The correct choice of k is of particular importance for the SVD method. A too-small value will bias the unfolding result towards the MC truth input, a too-large value will give a result that is dominated by unphysically enhanced statistical fluctuations. This needs to be tuned for any given distribution, number of bins, and approximate sample size -- with k between 2 and the number of bins. (Using k = 1 means you get only the training truth input as result without any corrections. You basically regularize away any differences, and only keep the leading term which is, by construction, the MC truth input.)"
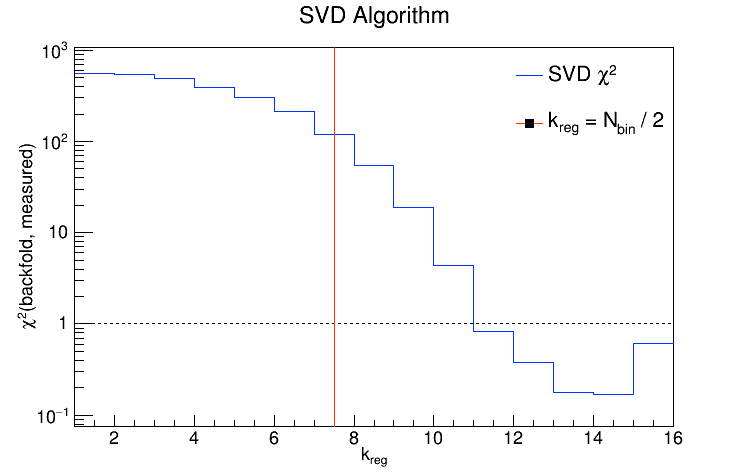
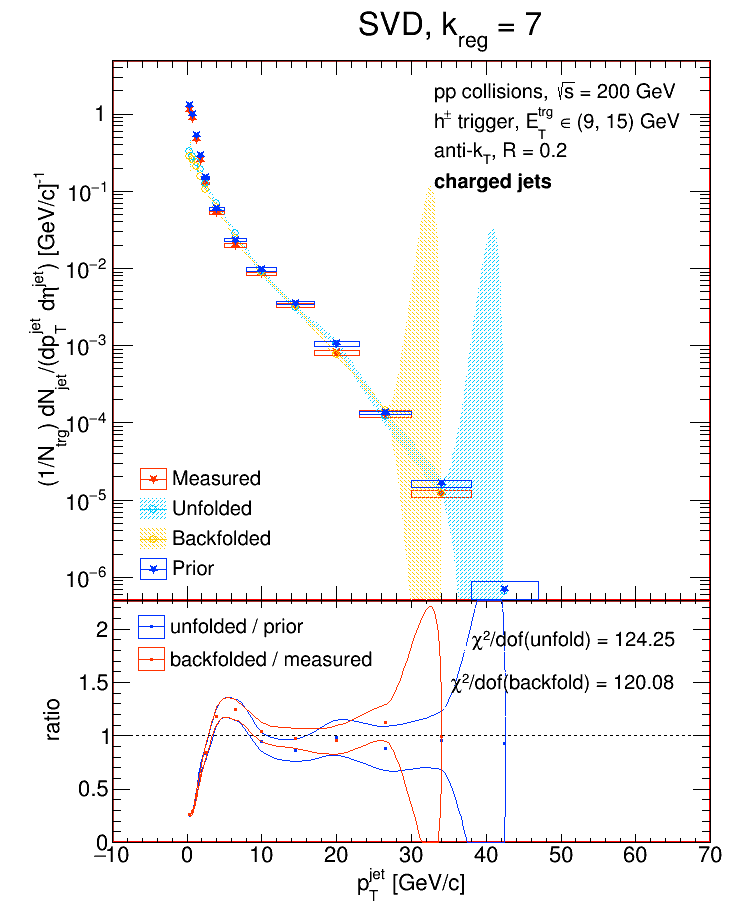
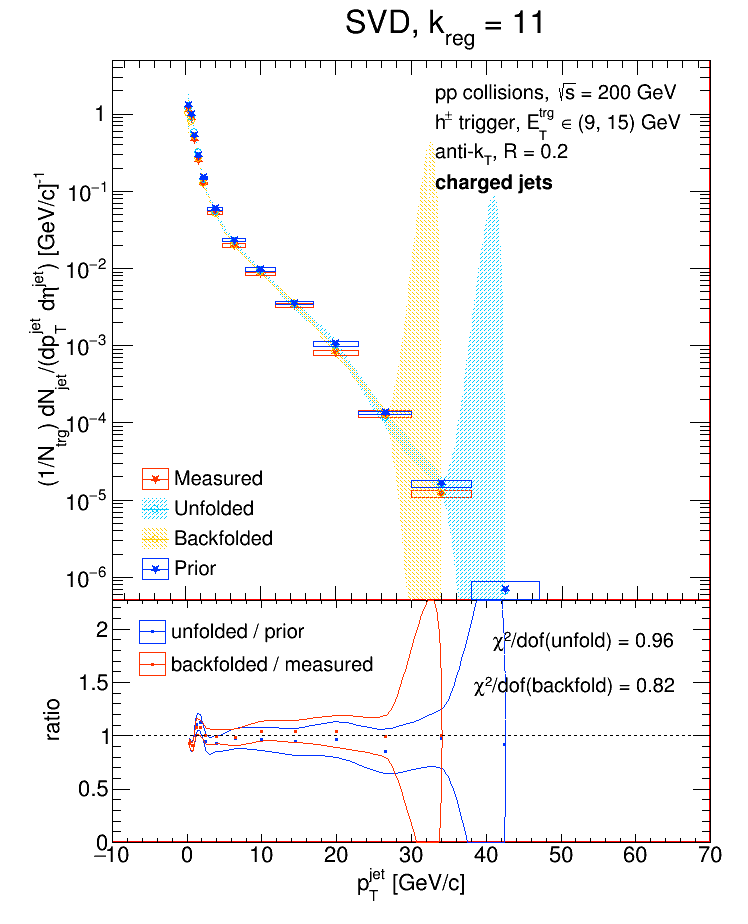
So a value of k = 12 is perfectly reasonable if the no. of bins you're using is, say, 17 or 26. In fact, the default value of k for the SVD algorithm is the no. of bins divided by 2. I tried unfolding the detector-level R = 0.2 charged jets from the Run9 dijet embedding sample and looked at the performance of the SVD algorithm as a function of k for two different binning schemes. In each case, I'll show the chi2 between the unfolded and truth (particle-level R = 0.2 charged jets) distributions, then the chi2 between the backfolded and measured (detector-level R = 0.2 charged jets), then the various distributions for k = Nbins / 2, and then the various distributions for the value of k which gave the best chi2.
Nbin = 15:

Nbin = 36:
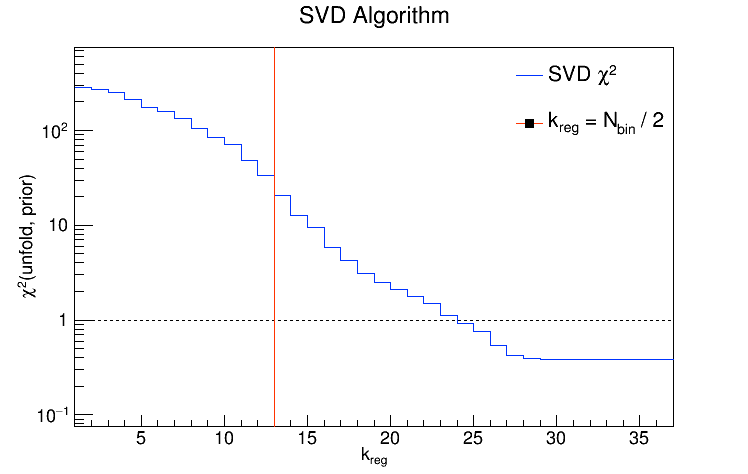
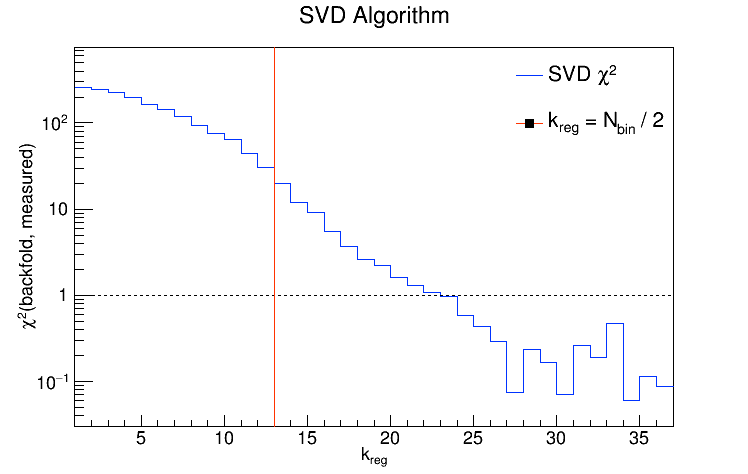
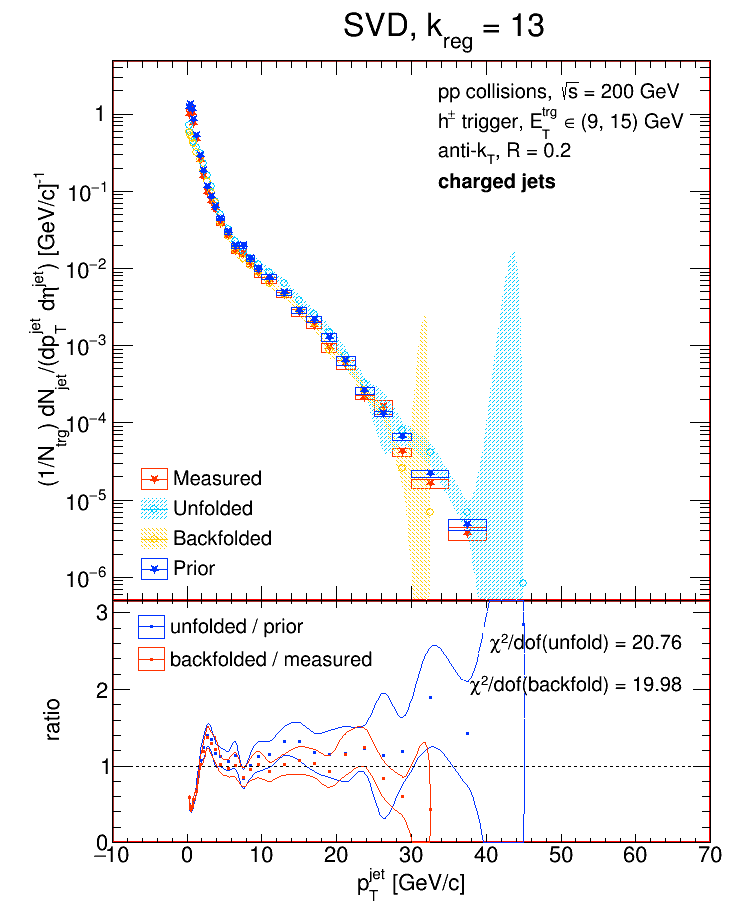
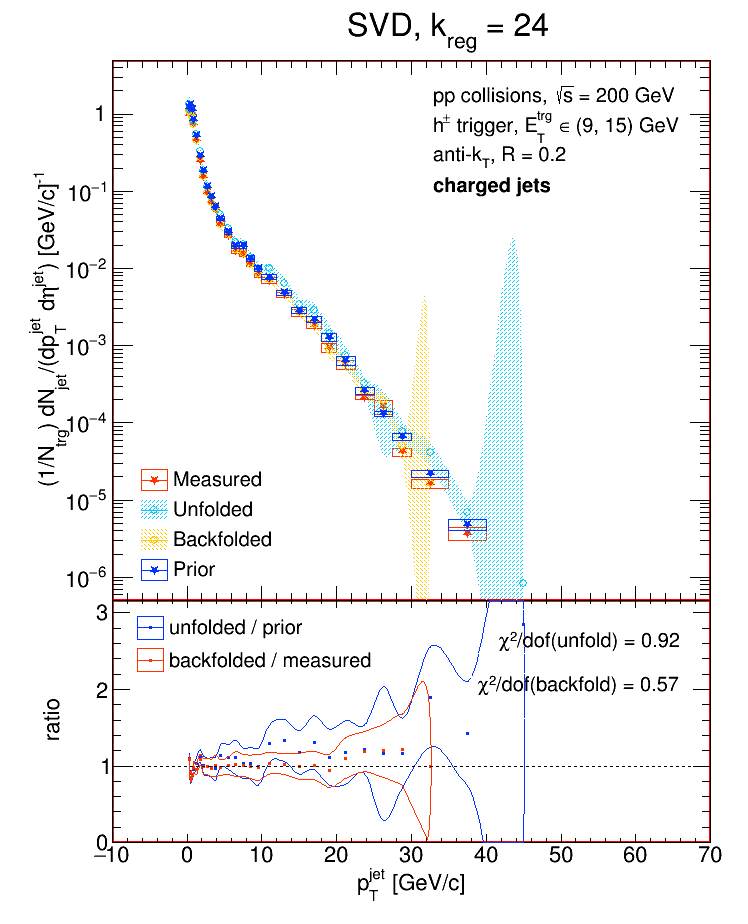
The exploding error bars on the last bin of each unfolded / backfolded distribution are just ROOT misbehaving.
- dmawxc's blog
- Login or register to post comments
